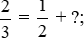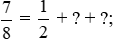Cho dãy số được xác định bởi:
với n là số tự nhiên khác 0.
a) Tính an với n =1,2,3,4,5,6. (kết quả viết dưới dạng phân số)
b) Tính a2012 (Lấy kết quả đúng)
( Gợi ý: - Nhân cả tử và mẫu của a2 với cùng 1 số rồi tách tử và mẫu thành tích, tương tự với a3. Từ đó tìm CTTQ của an)


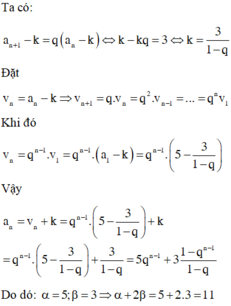
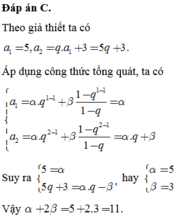

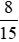 ; c)
; c)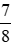 ; d)
; d)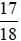 .
.