Cho tam giác ABC vuông tại A, BC=2AB. Giải tam giác ABC biết AC=4a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 12 2019
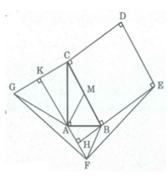
Gọi M là trung điểm của BC, ta có:
AM = MB = 1/2 BC = a (tính chất tam giác vuông)
Suy ra MA = MB = AB = a
Suy ra ∆ AMB đều ⇒ ∠ (ABC) = 60 0
Mặt khác: ∠ (ABC) + ∠ (ACB) = 90 0 (tính chất tam giác vuông)
Suy ra: ∠ (ACB) = 90 0 - ∠ (ABC) = 90 0 – 60 0 = 30 0
Trong tam giác vuông ABC, theo Pi-ta-go, ta có: B C 2 = A B 2 + A C 2
⇒ A C 2 = B C 2 - A B 2 = 4 a 2 - a 2 = 3 a 2 ⇒ AC = a 3
Vậy S A B C = 1/2 .AB.AC
= 1 2 a . a 3 = a 2 3 2 ( đ v d t )
3 tháng 12 2023
a: Kẻ DK\(\perp\)BC
Xét ΔBAD vuông tại A và ΔBKD vuông tại K có
BD chung
\(\widehat{ABD}=\widehat{KBD}\)
Do đó: ΔBAD=ΔBKD
=>BA=BK
mà \(BA=\dfrac{1}{2}BC\)
nên \(BK=\dfrac{1}{2}CB\)
=>K là trung điểm của BC
Xét ΔDBC có
DK là đường cao
DK là đường trung tuyến
Do đó: ΔDBC cân tại D
b: ΔDBC cân tại D
=>\(\widehat{DBC}=\widehat{DCB}\)
mà \(\widehat{DBC}=\dfrac{1}{2}\cdot\widehat{ABC}\)
nên \(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\dfrac{1}{2}\cdot\widehat{ABC}+\widehat{ABC}=90^0\)
=>\(\dfrac{3}{2}\cdot\widehat{ABC}=90^0\)
=>\(\widehat{ABC}=90^0:\dfrac{3}{2}=90^0\cdot\dfrac{2}{3}=60^0\)
\(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}=\dfrac{1}{2}\cdot60^0=30^0\)
T
14 tháng 8 2020
A B C D E
a, Xét tam giác AED và tam giác CED có :
cạnh ED chung
góc ADE = góc CDE = 90độ
AD = CD ( vì D là trung điểm cạnh AC )
Do đó : tam giác AED = tam giác CED ( c.g.c )
=> AE = CE ( cạnh tương ứng )
Vậy tam giác AEC cân tại E
b, Xét tam giác ABC có góc A = 90độ nên :
góc B + góc C = 90độ
mà góc C = góc EAC ( vì tam giác AEC cân theo câu a )
=> góc B + góc EAC = 90độ
Ta có : góc A = góc BAE + góc EAC = 90độ
=> góc B = góc BAE ( vì cùng phụ với góc EAC )
=> tam giác ABE cân tại E
=> AE = BE ( * )
mà AE = CE ( theo câu a )
=> BE = CE và điểm E nằm trên cạnh BC
=> E là trung điểm của BC
=> BE = CE = \(\frac{BC}{2}\) (1)
Theo bài cho : 2AB = BC
=> AB = \(\frac{BC}{2}\) (2)
Từ (1) và (2) suy ra : AB = BE và BE = AE ( theo ( * ) )
=> AB = BE = AE
Vậy tam giác ABE đều .
Học tốt
XO
14 tháng 8 2020
B A C M D E
Gọi M là trung điểm của BC
a) Xét 2 tam giác vuông : \(\Delta\)AED và \(\Delta\)CED có :
\(\hept{\begin{cases}AD=CD\left(gt\right)\\\widehat{EAD}=\widehat{EDC}\left(=90^{\text{o}}\right)\\ED\text{ chung}\end{cases}}\Rightarrow\Delta AED=\Delta CED\left(c.g.c\right)\)
=> AE = EC (cạnh tương ứng)
=> \(\Delta\)AEC cân tại E
b) Vì trong 1 tam giác vuông trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền
=> AM = 1/2 BC
=> AM = BM
Lại có BM = AB
=> AB = AM = BM
=> TAM GIÁC ABE đều
17 tháng 10 2021
\(BA=4\sqrt{3}\left(cm\right)\)
\(\widehat{A}=30^0\)
\(\widehat{C}=60^0\)
11 tháng 10 2021
Bài 1:
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
hay \(AB=\sqrt{13}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{6}{7}\)
nên \(\widehat{B}=59^0\)
hay \(\widehat{C}=31^0\)
28 tháng 7 2023
a: Sửa đề: tính AB
AB=căn 5^2-3^2=4cm
b: Xét ΔABC vuông tại A và ΔABD vuông tại A có
AB chung
AC=AD
=>ΔABC=ΔABD
c: ΔABC=ΔABD
=>BC=BD
=>ΔBCD cân tại B
Ta có:
\(sinC=\dfrac{AB}{BC}=\dfrac{AB}{2AB}=\dfrac{1}{2}\)
\(\Rightarrow\widehat{C}=30^o\)
Mà: \(\widehat{C}+\widehat{B}=90^o\Rightarrow\widehat{B}=90^o-\widehat{C}=90^o-30^o=60^o\)
Xét tam giác ABC vuông tại A có:
\(sinB=\dfrac{AC}{BC}=\dfrac{4a}{BC}\)
\(\Rightarrow BC=\dfrac{4a}{sinB}=\dfrac{4a}{sin60^o}=\dfrac{4a}{\dfrac{\sqrt{3}}{2}}=\dfrac{8a}{\sqrt{3}}=\dfrac{8\sqrt{3}a}{3}\)
\(\Rightarrow AC=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot\dfrac{8\sqrt{3}}{3}=\dfrac{8\sqrt{3}}{6}a=\dfrac{4\sqrt{3}}{3}a\)
Xét ΔABC vuông tại A có sin C=AB/BC=1/2
nên góc C=30 độ
=>góc B=90-30=60 độ
Xét ΔABC vuông tại A có sin B=AC/BC
=>4a/BC=sin60
=>\(BC=4a:sin60=\dfrac{8}{3}\sqrt{3}\cdot a\)
=>\(AC=\dfrac{1}{2}\cdot BC=\dfrac{4}{3}\cdot\sqrt{3}\cdot a\)