Tính tổng S=1/2+3/4+7/8+15/16+31/32+63/64+127/128-6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Q=\(\dfrac{1}{2}+\left(\dfrac{3}{4}+\dfrac{7}{8}\right)+\left(\dfrac{15}{16}+\dfrac{31}{32}\right)+\left(\dfrac{63}{64}+\dfrac{127}{128}\right)-6\)
Q=\(\dfrac{1}{2}+\dfrac{13}{8}+\dfrac{61}{32}+\dfrac{253}{128}\)\(-6\)
Q= \(\dfrac{64}{128}+\dfrac{208}{128}+\dfrac{244}{128}+\dfrac{253}{128}-6\)
Q= \(\dfrac{769}{128}-6\)
Q=\(\dfrac{769}{128}-\dfrac{768}{128}\)
Q= \(\dfrac{1}{128}\)

S1 = \(\frac{1}{2}+\frac{3}{4}+\frac{7}{8}+...+\frac{127}{128}\)
2S1 = 1 + \(\frac{3}{2}+\frac{7}{4}+\frac{15}{8}+\frac{31}{16}+\frac{63}{32}+\frac{127}{64}\)
2S1 - S1 = S1 = 1 + (1 + 1 + 1 + 1 + 1 + 1) - \(\frac{127}{128}\)= 6 + \(\frac{1}{128}\)
=> S = S1 - 6 = 6 + \(\frac{1}{128}\)- 6 = \(\frac{1}{128}\)
\(S=\frac{1}{2}+\frac{3}{4}+\frac{7}{8}+\frac{15}{16}+\frac{31}{32}+\frac{63}{64}+\frac{127}{128}-6\)
\(S=\frac{1}{2}+\left(\frac{3}{4}+\frac{7}{8}\right)+\left(\frac{15}{16}+\frac{31}{32}\right)+\left(\frac{63}{64}+\frac{127}{128}\right)-6\)
\(S=\frac{1}{2}+\frac{13}{8}+\frac{61}{32}+\frac{253}{128}-6\)
\(S=\frac{64}{128}+\frac{208}{128}+\frac{244}{128}+\frac{253}{128}-6\)
\(S=\frac{769}{128}-6\)
\(S=\frac{769}{128}-\frac{768}{128}\)
\(S=\frac{1}{128}\)
hok tốt!!


Cộng thêm 1/2 vào biểu thức đã cho, có:
S + 1/2= 1/2+1/4+ 1/8+ 1/16+1/32+1/64+1/128
Nhận xét:
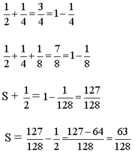

X x (1/2+1/4+1/8+1/16+1/32+1/64+1/128) = 127/128
X x 127/128 = 127/128
X = 127/128 : 127/128
X = 1

a) 19 + (29 - 9*37) - (63*9 - 29*99)
= 19 + 29 - 9*37 - 63*9 + 29*99
= 19 + 29(1 + 99) - 9(37 + 63)
= 19 + 29*100 - 9*100
= 19 + 100(29 - 9)
= 19 + 100*20
= 19 + 2000 = 2019
b) \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
= \(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}+\frac{1}{2^6}+\frac{1}{2^7}\)
= \(\frac{2^6+2^5+2^4+2^3+2^2+2+1}{2^7}\)
= \(\frac{64+32+16+8+4+2+1}{128}\) = \(\frac{127}{128}\)

b: A=1/3+1/9+...+1/3^10
=>3A=1+1/3+...+1/3^9
=>A*2=1-1/3^10=(3^10-1)/3^10
=>A=(3^10-1)/(2*3^10)
c: C=3/2+3/8+3/32+3/128+3/512
=>4C=6+3/2+...+3/128
=>3C=6-3/512
=>C=1023/512
d: A=1/2+...+1/256
=>2A=1+1/2+...+1/128
=>A=1-1/256=255/256

1/ 2 + 2 = 4
2/ 4 + 4 = 8
3/ 8 + 8 = 16
4/ 16 + 16 = 32
5/ 32 + 32 =64
6/ 64 + 64 =128
7/ 128 + 128 =256
8/ 256 + 256 =512
9/ 521 + 512 =1033
10/ 2048 + 2048 =4096
Ta có :
\(S=\left(\frac{1}{2}+\frac{3}{4}+\frac{7}{8}+\frac{15}{16}+\frac{31}{32}+\frac{63}{64}+\frac{127}{128}\right)-6\)
\(S=\left(\frac{64}{128}+\frac{102}{128}+\frac{112}{128}+\frac{120}{128}+\frac{124}{128}+\frac{126}{128}+\frac{127}{128}\right)-6\)
\(S=\frac{64+102+112+120+124+126+127}{128}-6\)
\(S=\frac{775}{128}-6\)
\(S=\frac{775}{128}-\frac{768}{128}\)
\(S=\frac{7}{128}\)
S=1/2+3/4+7/8+15/16+31/32+63/64+127/128 -6
S= 1-1/2 + 1-1/4 + 1-1/8 + 1-1/16 + 1-1/32 + 1-1/64+ 1-1/128 - 6
S= (1+1+1+1+1+1+1-6)- (1/2+1/4+1/8+1/16 + 1/32+1/64+1/128)
S= 1- 111/128
S= 17/128
(Làm lụi nha bn)