cho tam giác ABC và một điểm D trên cạnh BC. Chúng minh rằng AD.BC<AB.CD+AC.BD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Có AD // BM (gt), DM // AB (gt) => DA = BM; DM = AB ( tính chất đoạn chắn) (1)
AE // CM (gt); AC // EM (gt) => AE = CM; AC = EM ( tính chất đoạn chắn) (2)
Từ (1) và (2) => AD + AE = BM + CM
=> DE = BC
Xét ΔABCΔABC và ΔMDEΔMDE có:
AB = DM (cmt)
BC = DE (cmt)
AC = EM (cmt)
Do đó, ΔABC=ΔΔABC=ΔMDE (c.c.c)

Trong tam giác ABC ta có: DE // AC (gt)
Suy ra: 
Lại có: DF // AB (gt)
Suy ra: 
Cộng từng vế (1) và (2) ta có:
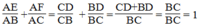

A B C D M E M F 1 2 1 2 3
Kẻ NF // AB (F thuộc BC)
Xét tam giác BEF và tam giác NFE có:
BEF = NFE (2 góc so le trong, NF // BE)
FE chung
EFB = FEN (2 góc so le trong, EN // FB)
=> Tam giác BEF = Tam giác NFE (g.c.g)
=> BE = NF (2 cạnh tương ứng)
mà BE = AD (gt)
=> AD = NF
Xét tam giác ADM và tam giác NFC có:
MDA = CFN (2 góc đồng vị, DM // FC)
DA = FN (chứng minh trên)
DAM = FNC (2 góc đồng vị, AD // NF)
=> Tam giác ADM = Tam giác NFC (g.c.g)
=> DM = FC (2 cạnh tương ứng)
mà EN = BF (tam giác BEF = tam giác NFE)
=> DM + EN = BF + FC = BC

Qua N kẻ đường thẳng song song với AB cắt BC tại K
Nối E với K
Xét \(\Delta BEC\)và \(\Delta NKE\)có:
\(\widehat{BEC}=\widehat{NKE}\)(BE//NC)
EC chung
\(\widehat{BCE}=\widehat{NEK}\)(EN//BC)
=>\(\Delta BCE=\Delta NKE\)(g-c-g)
=>EN=BK(1) ; EB=NK
vì DM//BC
=>\(\widehat{ADM}=\widehat{EBK}\)(2 góc đồng vị)
VìBA//NK
=>\(\widehat{EBK}=\widehat{NKC}\)(2 góc đồng vị) ; \(\widehat{BAN}=\widehat{KCN}\)(2 góc đồng vị)
Mà \(\widehat{EBK}=\widehat{ADM}\)=>\(\widehat{NKC}=\widehat{ADM}\)
Xét \(\Delta ADM\)và \(\Delta NKC\)có:
\(\widehat{MAD}=\widehat{CNK}\)
NK=AD(=BE)
\(\widehat{ADM}=\widehat{NKC}\)
=>\(\Delta ADM=\Delta NKC\left(g-c-g\right)\)
=>DM=KC(2)
Cộng 2 vế của (1),(2) ta được:
EN+DM=BK+KC
=>EN+DM=BC
Vậy EN+DM=BC

qua M kẻ đường thẳng song song với AB cắt BC tại I
Nối EC ; DI
xét tam giác BDI và tam giác NID có :
\(DI\) là cạnh chung
\(\widehat{DBI}=\widehat{DIN}\) (vì IN // AB)
\(\widehat{BID}=\widehat{IDN}\) ( DM // BC)
\(\Rightarrow BI=DN\) (2 cạnh tương ứng ) ( 1)
xét \(\Delta ADN\) và \(\Delta EBI\) CÓ:
AD=BE ( gt)
góc ADN = goác EBI ( DM//BC ; E,D thuộc AB )
BI=DN ( cmt )
\(\Rightarrow\widehat{BEI}=\widehat{DAN}\) (2 góc tương ứng )
hay \(\widehat{BEI}=\widehat{EAC}\) ( vì \(D,E\in AB;N\in AC\) )
mà \(\widehat{BEI}\) và \(\widehat{EAC}\) là 2 góc đồng vị
\(\Rightarrow EI\) // \(AC\)
xét \(\Delta EIC\) và \(\Delta CNI\) có :
\(\widehat{IEC}=\widehat{ECN}\) ( vì EI//AC)
EC chung
\(\widehat{ICF}=\widehat{CEN}\) ( vì EN // BC)
\(\Rightarrow\Delta EIC=\Delta CNI\) ( g.c.g)
\(\Rightarrow EN=IC\) ( 2 cạnh tương ứng ) ( 2)
từ (1 ) và (2) => DM+EN=IB+IC
=> DM+EN=BC ( I nằm giữa A và B ) (ĐPCM )