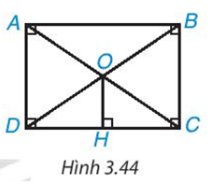
Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH ⊥ DC (H.3.44). Chứng minh rằng H là trung điểm của DC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 6 2023
a: Xét ΔBDE vuông tại D và ΔDCE vuông tại C có
góc E chung
=>ΔBDE đồng dạng với ΔDCE
b: BD=căn 8^2+6^2=10cm
BE=10^2/6=100/6=50/3cm
EC=DC^2/BC=8^2/6=32/3cm
Xét ΔEBD có CH//BD
nên CH/BD=EC/EB
=>CH/10=32/50=16/25
=>CH=160/25=6,4cm
2 tháng 3 2023
a: Xét ΔBDE vuông tại D và ΔDCE vuông tại C có
góc E chung
=>ΔBDE đồng dạng với ΔDCE
b: Xét ΔHDC vuông tại H và ΔDBE vuông tại D có
góc HDC=góc DBE
=>ΔHDC đồng dạng với ΔDBE
=>DH/DB=CH/DE
=>DH*DE=CB*CH=DC^2
c: DC^2=CH*DB
=>CH*10=8^2=64
=>CH=6,4cm
\(DH=\sqrt{8^2-6.4^2}=4.8\left(cm\right)\)
=>DE=8^2/4,8=40/3(cm)
=>CE=32/3(cm)
Xét ΔHCE vuông tại H và ΔCDE vuông tại C có
góc HEC chung
=>ΔHCE đồng dạng với ΔCDE
=>\(\dfrac{S_{HCE}}{S_{CDE}}=\left(\dfrac{CE}{DE}\right)^2=\left(\dfrac{32}{3}:\dfrac{40}{3}\right)^2=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)
27 tháng 10 2021
b: Xét ΔADK vuông tại K và ΔCBH vuông tại H có
AD=CB
\(\widehat{ADK}=\widehat{CBH}\)
Do đó: ΔADK=ΔCBH
Suy ra: DK=BH
Xét tứ giác BKDH có
DK//BH
DK=BH
Do đó: BKDH là hình bình hành
6 tháng 1 2021
a) Ta có: \(\widehat{BCD}+\widehat{BCN}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{BCN}=180^0-\widehat{BCD}=180^0-90^0\)
\(\Leftrightarrow\widehat{BCN}=90^0\)
hay \(\widehat{MCN}=90^0\)
Xét tứ giác MCNF có
\(\widehat{MCN}=90^0\)(cmt)
\(\widehat{FMC}=90^0\)(FM⊥BC)
\(\widehat{FNC}=90^0\)(FN⊥DC)
Do đó: MCNF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: ABCD là hình chữ nhật(gt)
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường và bằng nhau(Định lí hình chữ nhật)
mà AC cắt BD tại O(gt)
nên O là trung điểm chung của AC và BD; AC=BD
Xét ΔACF có
O là trung điểm của AC(cmt)
E là trung điểm của AF(gt)
Do đó: OE là đường trung bình của ΔACF(Định nghĩa đường trung bình của tam giác)
⇒OE//CF và \(OE=\dfrac{CF}{2}\)(Định lí 2 về đường trung bình của tam giác)
hay CF//BD(đpcm)
Xét tam giác DBC, ta có:
O là trung điểm cạnh BD (tính chất hình chữ nhật)
OH // BC (cùng vuông góc với CD)
⇒ OH là đường trung bình tam giác BCD.
⇒ H là trung điểm của CD (đpcm).