Tìm hàm số bậc nhất y = ax + b (a≠0) trong mỗi trường hợp sau:
a) Đồ thị của hàm số đó đi qua điểm M (1; 3) và có hệ số góc bằng -2.
b) Đồ thị của hàm số đó đi qua điểm N (-1; 4) và song song với đường thẳng y = -3x – 1.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 10 2021
a: Vì (d) song song với y=3x+1 nên a=1
Vậy: (d): y=x+b
Thay x=2 và y=5 vào (d), ta được:
b+2=5
hay b=3
b: Theo đề,ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=2\\2a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=5\\a-b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=a+2=\dfrac{-5}{3}+2=\dfrac{1}{3}\end{matrix}\right.\)
CM
2 tháng 12 2017
Với a = 3 hàm số có dạng y = 3x + b.
Đồ thị hàm số đi qua điểm (2; 2), nên ta có:
2 = 3.2 + b => b = 2 – 6 = - 4
Vậy hàm số là y = 3x – 4
CM
1 tháng 2 2018
a) Với a = 2 hàm số có dạng y = 2x + b.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5 khi đó tung độ bằng 0 nên:
0 = 2.1,5 + b => b = -3
Vậy hàm số là y = 2x – 3
b) Với a = 3 hàm số có dạng y = 3x + b.
Đồ thị hàm số đi qua điểm (2; 2), nên ta có:
2 = 3.2 + b => b = 2 – 6 = - 4
Vậy hàm số là y = 3x – 4
c) Đường thẳng y = ax + b song song với đường thẳng y = √3 x nên a = √3 và b ≠ 0. Khi đó hàm số có dạng y = √3 x + b
Đồ thị hàm số đi qua điểm (1; √3 + 5) nên ta có:
√3 + 5 = √3 . 1 + b => b = 5
Vậy hàm số là y = √3 x + 5
CM
5 tháng 4 2018
Đường thẳng y = ax + b song song với đường thẳng y = √3 x nên a = √3 và b ≠ 0. Khi đó hàm số có dạng y = √3 x + b
Đồ thị hàm số đi qua điểm (1; √3 + 5) nên ta có:
√3 + 5 = √3 . 1 + b => b = 5
Vậy hàm số là y = √3 x + 5
CC
28 tháng 10 2017
a, ĐỒ thị hàm số (1) đi qua điểm M(1/2;-2 )
<=> -2 = 1/2.a -3
<=> 1/2.a= -2+3
<=> 1/2.a = 1
<=> a = 2
b, Ta có tọa độ giao điểm của đồ thị hàm số ( 1) và độ thị hàm số y= - 3x + 2 ( đặt là 1' )là nghiệm của hệ phương trình :
\(\hept{\begin{cases}ax-3=-3x+2\\y=ax-3\end{cases}}\)mà (1 ) cắt (1') tại điểm có tung độ bằng 5 => y =5 => Ta có : \(\hept{\begin{cases}ax-3=-3x+2\\5=ax-3\end{cases}\Leftrightarrow\hept{\begin{cases}a.\frac{8}{a}-3=-3.\frac{8}{a}+2\\x=\frac{8}{a}\end{cases}}\Leftrightarrow a=-8}\)
20 tháng 9 2021
a: Vì hệ số góc là 2 nên a=2
Thay x=0 và y=2 vào y=2x+b, ta được:
b+0=2
hay b=2
12 tháng 9 2023
a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
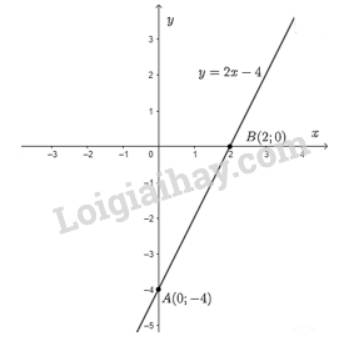
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).
a) Đồ thị hàm số y = ax + b (a\( \ne \)0) có hệ số góc bằng -2 nên a = -2
Suy ra hàm số bậc nhất là y = -2x + b
Đồ thị hàm số y = -2x + b đi qua điểm M(1; 3) nên ta có:
3 = -2 .1+b suy ra b = 5
Vậy hàm số bậc nhất cần tìm là: y = -2x + 5
b) Đồ thị hàm số y = ax + b (a\( \ne \)0) song song với đường thẳng y = -3x -1 nên a = -3, b \(\ne\) -1
Suy ra hàm số bậc nhất là y = -3x + b
Đồ thị hàm số y = -3x + b đi qua điểm N(-1; 4) nên ta có:
4 = -3. (-1) + b suy ra b = 1
Vậy hàm số bậc nhất cần tìm là y = -3x + 1