Cho tam giác ABC nhọn (AB < AC) , vẽ đường tròn tâm O đường kính BC cắt AB và AC tại D và E, CD cắt BE tại H. a) Chứng minh AH vuông góc BC. b) Chứng minh 4 điểm A, E, H, D cùng thuộc một đường đường tròn, xác định tâm I của đường tròn qua 4 điểm. c) Chứng minh 4 điểm B, C, D, E cùng thuộc 1 đường tròn. Xác định tâm O của đường tròn đi qua 4 điểm d) Chứng minh OI vuông góc với DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 9 2023
a: Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
=>CF vuông góc AB
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE vuông góc AC
Xét ΔABC có
BE,CF là đường cao
BE cắt CF tại H
Do đó: H là trực tâm
=>AH vuông góc BC tại D
b: Xét tứ giác AFHE có
góc AFH+góc AEH=90+90=180 độ
=>AFHE nội tiếp đường tròn đường kính AH
I là trung điẻm của AH
c:
Xét tứ giác BFHD có
góc BFH+góc BDH=180 độ
=>BFHD nội tiếp
=>góc DFH=góc DBH=góc EBC
góc IFD=góc IFH+góc DFH
=góc IHF+góc EBC
=góc DHC+góc EBC
=90 độ-góc FCB+góc EBC
=90 độ
=>IF là tiếp tuyến của (O)
Xét ΔIFD và ΔIED có
IF=IE
FD=ED
ID chung
=>ΔIFD=ΔIED
=>góc IED=góc IFD=90 độ
=>IE là tiếp tuyến của (O)
31 tháng 1
a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>CD\(\perp\)AB tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó;ΔBEC vuông tại E
=>BE\(\perp\)AC tại E
Xét ΔABC có
BE,CD là các đường cao
BE cắt CD tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
Xét tứ giác HECF có \(\widehat{HEC}+\widehat{HFC}=90^0+90^0=180^0\)
nên HECF là tứ giác nội tiếp
=>\(\widehat{HEF}=\widehat{HCF}\)
15 tháng 11 2023
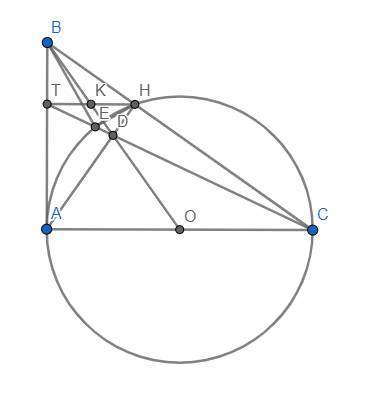
Gọi T là giao điểm của CD và AB. Khi đó xét tứ giác ACHT, ta có:
O (trung điểm AC), D (giao điểm của 2 đường chéo) và B (giao điểm của 2 đường thẳng chứa 2 cạnh đối) thẳng hàng nên ACHT là hình thang. (bổ đề hình thang quen thuộc)
\(\Rightarrow\) HT//AC \(\Rightarrow\) H, K, T thẳng hàng.
Lại có \(\widehat{CEH}=\widehat{CAH}\) (góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{CAH}=\widehat{B}\) (cùng phụ với góc C)
\(\Rightarrow\widehat{CEH}=\widehat{B}\)
\(\Rightarrow\) Tứ giác BTEH nội tiếp \(\Rightarrow\widehat{BEH}=\widehat{BTH}\)
Mà \(\widehat{BTH}=90^o\) nên \(\widehat{BEH}=90^o\). Ta có đpcm.
29 tháng 11 2023
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>CD\(\perp\)DB tại D
=>CD\(\perp\)AB tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)AC tại E
Xét ΔABC có
BE,CD là đường cao
BE cắt CD tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
3 tháng 12 2021
a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: AH⊥BC
31 tháng 10 2021
a: Xét (O) có
ΔBDC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBEC vuông tại E
30 tháng 1 2021
a) Xét (O) có
ΔDBC nội tiếp đường tròn(D,B,C∈(O))
BC là đường kính(gt)
Do đó: ΔDBC vuông tại D(Định lí)
⇒CD⊥BD tại D
⇒CD⊥AB tại D
⇒HD⊥AD tại D
Xét ΔADH có HD⊥AD tại D(cmt)
nên ΔADH vuông tại D(Định nghĩa tam giác vuông)
Ta có: ΔADH vuông tại D(cmt)
mà DI là đường trung tuyến ứng với cạnh huyền AH(I là trung điểm của AH)
nên \(DI=\dfrac{AH}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(1)
Xét (O) có
ΔBEC nội tiếp đường tròn(B,E,C∈(O))
BC là đường kính(gt)
Do đó: ΔBEC vuông tại E(Định lí)
⇒BE⊥CE tại E
⇒BE⊥AC tại E
⇒HE⊥AE tại E
Xét ΔAEH có AE⊥EH tại E(cmt)
nên ΔAEH vuông tại E(Định nghĩa tam giác vuông)
Ta có: ΔAEH vuông tại E(cmt)
mà EI là đường trung tuyến ứng với cạnh huyền AH(I là trung điểm của AH)
nên \(EI=\dfrac{AH}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(2)
Từ (1) và (2) suy ra ID=IE
hay I nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OD=OE(=R)
nên O nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(4)
Từ (3) và (4) suy ra OI là đường trung trực của DE
hay OI⊥DE(đpcm)
a:
góc BDC=góc BEC=1/2*sđ cung BC=90 độ
=>CD vuông góc AB và BE vuông góc AC
Xét ΔABC có
CD,BE là đường cao
CD cắt BE tại H
=>H là trực tâm
=>AH vuông góc BC
b: góc AEH+góc ADH=180 độ
=>AEHD nội tiếp đường tròn đường kính AH
=>I là trung điểm của AH
c: góc BDC=góc BEC=90 độ
=>BDEC nội tiếp đường tròn đường kính BC
=>O là trung điểm của BC
d: ID=IE
OD=OE
=>OI là trung trực của DE
=>OI vuông góc DE