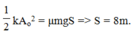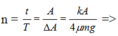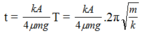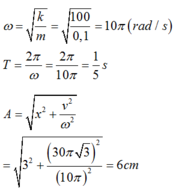Cho con lắc lò xo dao động trên mặt phẳng nằm ngang không ma sát như trong Hình 2. Con lắc lò xo thực hiện mỗi dao động mất 2,4 s. Tại t = 0, vật bắt đầu dao động từ chỗ cách vị trí cân bằng x = 3 cm.
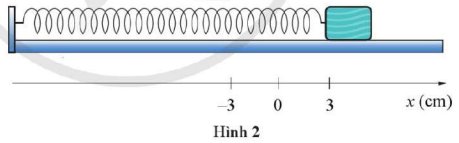
a) Tìm vị trí và vận tốc của vật tại thời điểm 0,60 s.
b) Tìm vị trí và vận tốc của vật tại thời điểm 1,20 s.