Dựa vào biểu thức (3.2) và (3.5), hãy thiết lập biểu thức (3.7).
\(W_t=\dfrac{1}{2}Kx^2=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t+\varphi_0\right)\) (3.2)
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t+\varphi_0\right)\) (3.5)
\(W_t+W_đ=\dfrac{1}{2}m\omega^2A^2\) (3.7)

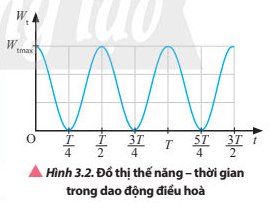

Ta có:
\(W_t=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t+\varphi_0\right)\\ W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t+\varphi_0\right)\\ \Rightarrow W=W_t+W_d=\dfrac{1}{2}m\omega^2A^2\left[cos^2\left(\omega t+\varphi_0\right)+sin^2\left(\omega t+\varphi_0\right)\right]\\ \Rightarrow W=\dfrac{1}{2}m\omega^2A^2\)