Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đề dài thế này sao giải thích nhanh cho e đc
Part 1
1 C
2 B
3 D
4 C
5 B
6 A
Part 2
1 T
2 F
3 F
4 F
V
1 That old house has just been bought
2 If he doesn't take these pills, he won't be better
3 I suggest taking a train
4 Spending the weekend in the countryside is very wonderful

Lời giải:
a. Áp dụng hệ thức lượng trong tam giác vuông ta có:
$AH^2=BH.CH=4.6=24$
$\Rightarrow AH=\sqrt{24}=2\sqrt{6}$ (cm)
$AB^2=BH.BC=BH(BH+CH)=4(4+6)=40$
$\Rightarrow AB=\sqrt{40}=2\sqrt{10}$ (cm)
b.
$AC^2=CH.BC=6(6+4)=60$
$\Rightarrow AC=\sqrt{60}=2\sqrt{15}$ (cm)
$AM=AC:2=\sqrt{15}$ (cm)
$\tan \widehat{AMB}=\frac{AB}{AM}=\frac{2\sqrt{10}}{\sqrt{15}}=\frac{2\sqrt{6}}{3}$
$\Rightarrow \widehat{AMB}=59^0$
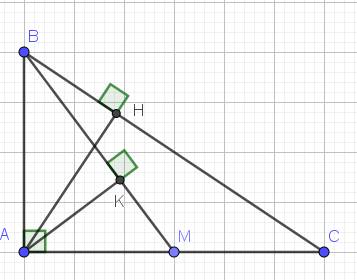
c.
Áp dụng hệ thức lượng trong tam giác vuông với tam giác $ABM$:
$BK.BM=AB^2(1)$
Áp dụng hệ thức lượng với tam giác $ABC$:
$AB^2=BH.BC(2)$
Từ $(1); (2)\Rightarrow BK.BM=BH.BC$


1 The meeting was canceled 3 days ago
2 She told me she was watching a film with her sister then
3 I admire the guitarist who is perfroming on the stage
4 Had it not been for Pauline's interest, the project would have been abandoned

a, Xét tứ giác ADHE có ^ADH = ^AEH = ^DAE = 900
=> tứ giác ADHE là hcn
=> AH = DE (2 đường chéo bằng nhau)
b, Xét tam giác AHB và tam giác CHA ta có
^AHB = ^CHA = 900
^HAB = ^HCA ( cùng phụ ^HAC )
Vậy tam giác AHB~ tam giác CHA (g.g)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=BH.CH\)
c, Xét tam giác AHD và tam giác ABH có
^ADH = ^AHB = 900
^A _ chung
Vậy tam giác AHD ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AD}{AH}\Rightarrow AH^2=AD.AB\)(1)
tương tự tam giác AEH ~ tam giác AHC (g.g)
\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\Rightarrow AH^2=AE.AC\left(2\right)\)
Từ (1) ; (2) suy ra \(AD.AB=AE.AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét tam giác ADE và tam giác ACB
^A _ chung
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\left(cmt\right)\)
Vậy tam giác ADE ~ tam giác ACB (c.g.c)

a.
\(n_S=\dfrac{16}{32}=0,5mol\)
Gọi \(\left\{{}\begin{matrix}n_{Zn}=x\\n_{Mg}=y\end{matrix}\right.\)
\(Zn+S\rightarrow\left(t^o\right)ZnS\)
x x ( mol )
\(Mg+S\rightarrow\left(t^o\right)MgS\)
y y ( mol )
Ta có:
\(\left\{{}\begin{matrix}65x+24y=23,4\\x+y=0,5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{57}{205}\\y=\dfrac{91}{410}\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}m_{Zn}=\dfrac{57}{205}.65=\dfrac{741}{41}g\\m_{Mg}=\dfrac{91}{410}.24=\dfrac{1092}{205}g\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}\%m_{Zn}=\dfrac{741}{41}:23,4.100=77,23\%\\\%m_{Mg}=100\%-77,23\%=22,77\%\end{matrix}\right.\)
b.\(ZnS+2HCl\rightarrow ZnCl_2+H_2S\)
57/205 57/205 ( mol )
\(MgS+2HCl\rightarrow MgCl_2+H_2S\)
91/410 91/410 ( mol )
\(V_{H_2S}=\left(\dfrac{57}{205}+\dfrac{91}{410}\right).22,4=11,2l\)