Mọi người giúp mình với ajaa <3
K
Khách
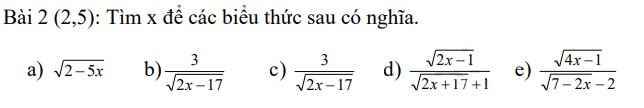
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2021
Hiệu quả phép so sánh: Thể hiện sự mong ngóng đến gần như tuyệt vọng của đứa con khao khát tình mẹ đến cháy bỏng.
7 tháng 8 2021
Tham khảo:
Đây là một phép so sánh mang ý nghĩa giả định, đầy mới lạ nhưng có giá trị to lớn trong việc thể hiện tâm trạng của nhân vật bé Hồng từ sự hi vọng đến sự tuyệt vọng đến đỉnh điểm. Bóng dáng, hình ảnh của người mẹ khi xuất hiện trước cặp mắt và nỗi niềm chờ mong trông đợi, mỏi mòn của đứa con cũng giống như dòng suối trong suốt chảy dưới bóng râm đang dần xuất hiện trước con mắt gần rạn nứt, tuyệt vọng của người bộ hành ngã gục giữa sa mạc khô hạn và nóng nực. Và để rồi, với việc sử dụng phép so sánh này tác giả đã diễn tả một cách chân thực và rõ nét nỗi khao khát, chờ mong được gặp mẹ, khao khát tình mẹ đến tột cùng trong nỗi lòng của đứa trẻ mồ côi, đã suốt một thời gian dài không được gặp mẹ, không được sà vào vòng tay yêu thương, ấm áp của mẹ. Nỗi khao khát ấy lớn đến mức nếu như người phụ nữ kia không phải là mẹ thì đứa bé tội nghiệp ấy sẽ thất vọng biết bao nhiêu, rồi nó sẽ ngã quỵ xuống như những "người bộ hành ngã gục giữa sa mạc khô hạn và nóng nực".
5 tháng 12 2021
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)
5 tháng 10 2021
Bài 2:
Lũy thừa với số mũ chẵn của một số hữu tỉ âm là số dương
Lũy thừa với số mũ lẻ của một số hữu tỉ âm là số âm
5 tháng 10 2021
Bài 13:
a: \(x^3=343\)
nên x=7
b: \(\left(2x-3\right)^2=9\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
5 tháng 10 2021
a: \(A=\dfrac{4^2\cdot4^3}{2^{10}}=\dfrac{4^5}{2^{10}}=1\)
b: \(C=\dfrac{5^4\cdot20^4}{25^5\cdot4^5}=\dfrac{100^4}{100^5}=\dfrac{1}{100}\)
\(e,\dfrac{\sqrt{4x-1}}{\sqrt{7-2x}-2}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}4x-1\ge0\\7-2x\ne4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{4}\\x\ne-\dfrac{3}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{1}{4}\)
\(d,\dfrac{\sqrt{2x-1}}{\sqrt{2x+17}+1}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}2x-1\ge0\\2x+17\ge0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{2}\\x\ge-\dfrac{17}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{1}{2}\)
\(b,c,\dfrac{3}{\sqrt{2x-17}}\) có nghĩa \(\Leftrightarrow2x-17>0\Leftrightarrow x>\dfrac{17}{2}\)
\(a,\sqrt{2-5x}\) có nghĩa \(\Leftrightarrow2-5x\ge0\Leftrightarrow x\le\dfrac{2}{5}\)