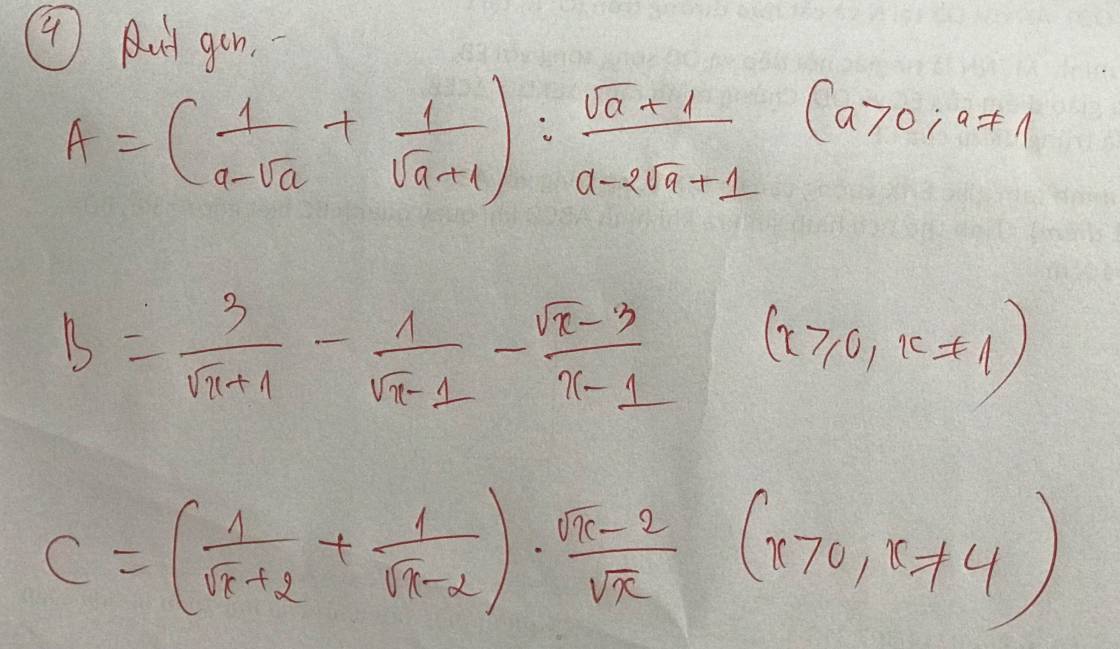Cho mình câu trả lời chi tiết mình đang cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 11 2021
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)
26 tháng 12 2021
\(a,=\dfrac{2y}{x}\\ b,=\dfrac{3\left(x+4\right)}{4\left(x-4\right)}\cdot\dfrac{-2\left(x-4\right)}{x+4}=\dfrac{-3}{2}\\ c,=\dfrac{\left(x+2\right)^2}{2\left(x-3\right)}\cdot\dfrac{x-3}{x+2}=\dfrac{x+2}{2}\\ d,=\dfrac{x+4+2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{3x}{x^2-4}\)
L
26 tháng 12 2021
a, \(\dfrac{2y}{x}\)
b, \(\dfrac{3\left(x+4\right)}{4\left(x-4\right)}.\dfrac{-2\left(x-4\right)}{x+4}=\dfrac{-3}{2}\)
c, \(\dfrac{\left(x+2\right)^2}{2\left(x-3\right)}.\dfrac{x-3}{x+2}=\dfrac{x+2}{2}\)
d, \(\dfrac{x+4}{\left(x-2\right)\left(x+2\right)}+\dfrac{2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{x+4+2x-4}{\left(x+2\right)\left(x-2\right)}=\dfrac{3x}{x^2-4}\)
PT
2
20 tháng 12 2021
mí cái đáp án trên là mk tính bừa ra nên ko đúng thì bn thông cảm hen
GH
22 tháng 6 2023
Với m = 3 thì (d): y = 8x - 7
PTHĐGĐ của (P) và (d): \(x^2-8x+7=0\)
Có: \(a+b+c=1+\left(-8\right)+7=0\)
=> PT có 2 nghiệm phân biệt \(x_1=1;x_2=7\)
\(x_1=1\Rightarrow y_1=x_1^2=1^2=1\\ x_2=7\Rightarrow y_2=x_2^2=7^2=49\)
Tọa độ giao điểm của (P) và (d) là: \(\left(1;1\right);\left(7;49\right)\)
b)
PTHĐGĐ của (P) và (d) là:
\(x^2-2\left(m+1\right)x+3m-2=0\)
\(\Delta'=\left(m+1\right)^2-\left(3m-2\right)=m^2+2m+1-3m+2=m^2-m+3\\ =m^2-m+\dfrac{1}{4}+\dfrac{11}{4}=\left(m-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall m\)
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=3m-2\end{matrix}\right.\)
Theo đề: \(x_1^2+x_2^2=20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4=20\\ \Leftrightarrow4m^2+2m+8-20=0\\ \Leftrightarrow4m^2+2m-12=0\\ \Leftrightarrow2m^2+m-6=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=-2\left(tm\right)\\m=\dfrac{3}{2}\left(tm\right)\end{matrix}\right.\)
Y
22 tháng 6 2023
Gọi tọa độ của \(\left(P\right),\left(d\right)\) là \(A\left(x_A;y_A\right),B\left(x_B;y_B\right)\)
\(a,m=3\)
\(\Rightarrow x^2=2\left(3+1\right)x-3.3+2\)
\(\Rightarrow x^2-8x+7=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=7\\x=1\end{matrix}\right.\)
Thay \(x=7\) vào \(\left(P\right):y=x^2\Rightarrow y=7^2=49\)
Khi m = 3 thì đường thẳng \(\left(d\right):y=2\left(3+1\right)x-3.3+2=8x-7\)
Thay \(x=1\) vào \(\left(d\right):y=8x-7=8.1-7=1\)
Vậy \(A\left(7;49\right),B\left(1;1\right)\)
\(\Rightarrow y=\left(2m+2\right)x-3m+2\)
\(b,\) Vì \(\left(P\right)\) và \(\left(d\right)\) luôn cắt nhau tại 2 điểm pb A,B \(\forall m\) nên :
\(x^2=2\left(m+1\right)x-3m+2\Leftrightarrow x^2-2\left(m+1\right)x+3m-2\)
Theo Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+2\\x_1x_2=\dfrac{c}{a}=3m-2\end{matrix}\right.\)
Ta có : \(x_1^2+x_2^2=20\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2\)
\(\Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4-20=0\)
\(\Leftrightarrow4m^2+2m-12=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m=-2\end{matrix}\right.\)
Vậy \(m=\dfrac{3}{2},m=-2\) thì thỏa mãn đề bài.
22 tháng 12 2021
bạn giúp mình đi mà mình bị mất sgk nên mới hỏi mọi người đó chứ mình àm còn thì mình đâu có hỏi đâu
14 tháng 1 2022
Bài 5:
a: Xét ΔABM và ΔDBM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔABM=ΔDBM
Suy ra: MA=MD
b: Ta có: ΔABM=ΔDBM
Suy ra: \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
c: \(\widehat{AMD}=180^0-60^0=120^0\)
nên \(\widehat{BMD}=60^0\)
MS
3
HN
9 tháng 11 2016
Xương có hai đặc tính (tính chất) cơ bản: mềm dẻo và bền chắc. Nhờ tính mềm dẻo nên xương có thể chống lại tất cả các lực cơ học tác động vào cơ thể, nhờ tính bền chắc mà bộ xương có thể nâng đỡ cơ thể.
- Xương có hai tính chất trên là nhờ vào thành phần hóa học. Xương được cấu tạo từ 2 chất chính: một loại chất hữu cơ gọi là cốt giao và một số chất vô cơ (chủ yếu là các muối can-xi) hay còn gọi là chất khoáng. Chất khoáng làm cho xương bền chắc, cốt giao đảm bảo tính mềm dẻo.
8 tháng 11 2016
Tính chất của xương là: Chất khoáng làm cho xương bền,chắc còn chất cốt giao đảm bảo tính mềm dẻo cho xương.
DT
3
NA
9 tháng 2 2022
\(a,=\dfrac{12\times\left(4+6\right)}{24}=\dfrac{12\times10}{24}=\dfrac{120}{24}=5\\ b,=\dfrac{16\times\left(8-2\right)}{48}=\dfrac{16\times6}{48}=\dfrac{96}{48}=2\)
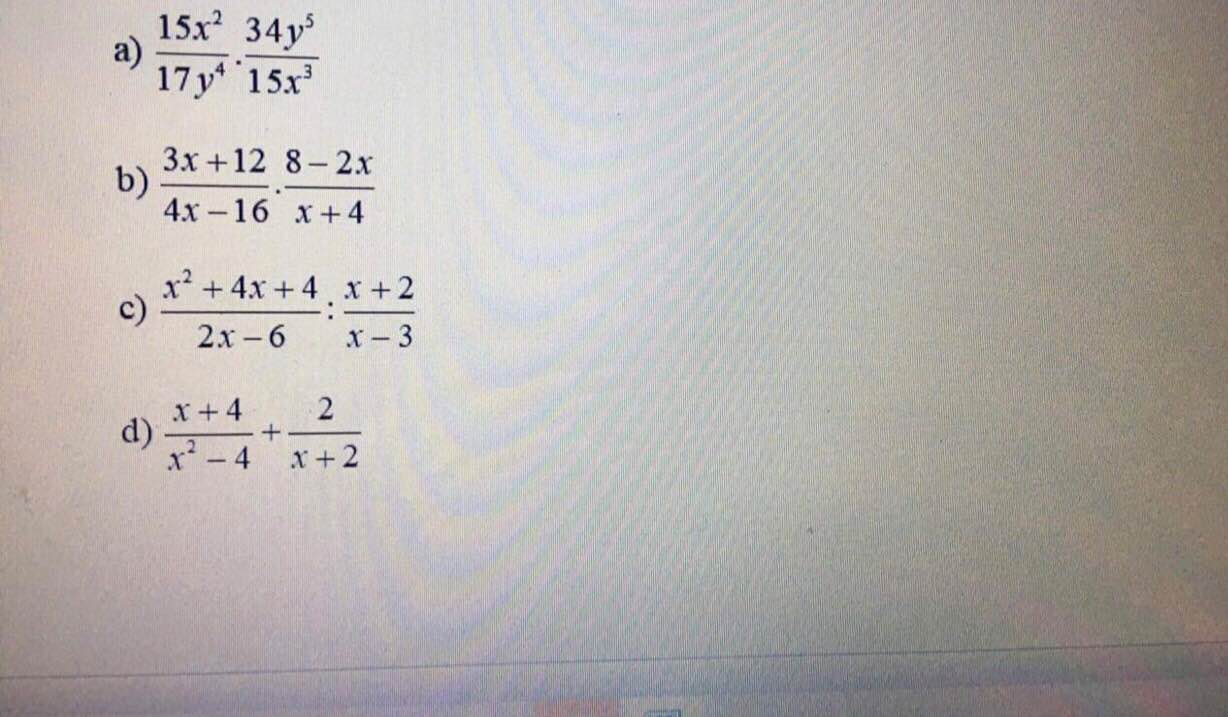
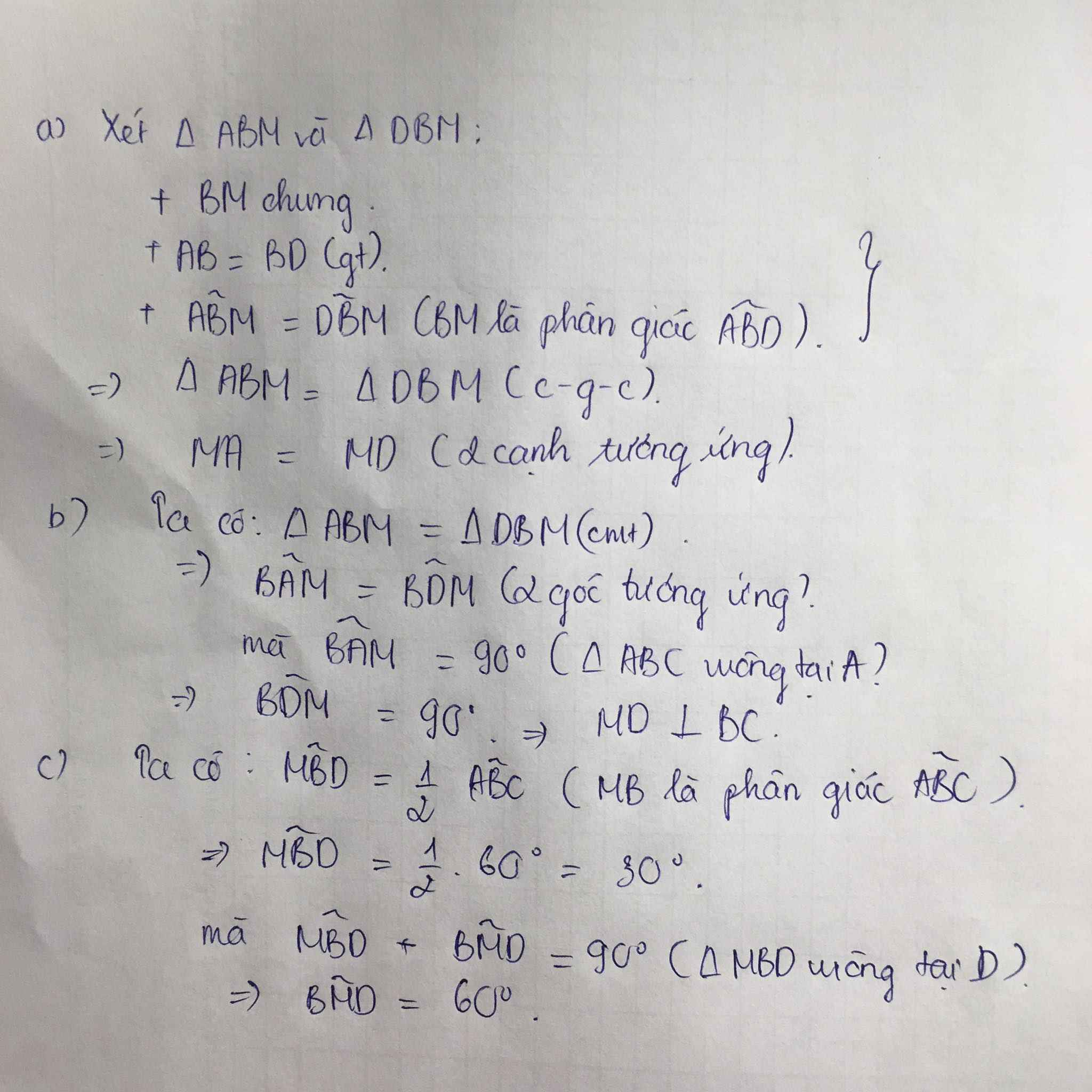
\(A=\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}+1}\right):\dfrac{\sqrt{a}+1}{a-2\sqrt{a}+1}\left(dkxd:a>0,a\ne1\right)\)
\(=\dfrac{\sqrt{a}+1+a-\sqrt{a}}{\left(a-\sqrt{a}\right)\left(\sqrt{a}+1\right)}.\dfrac{\sqrt{a^2}-2\sqrt{a}+1}{\sqrt{a}+1}\)
\(=\dfrac{1+a}{\sqrt{a}\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}.\dfrac{\left(\sqrt{a}-1\right)}{\sqrt{a}+1}\)
\(=\dfrac{1+a}{\sqrt{a}\left(\sqrt{a}+1\right)^2}\)
\(B=\dfrac{3}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\left(dkxd:x\ge0,x\ne1\right)\)
\(=\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{1+\sqrt{x}-3}{\sqrt{x}-1}\)
\(=\dfrac{3\sqrt{x}-3-\left(1+\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}-3-\sqrt{x}-1-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{1}{\sqrt{x}+1}\)
\(C=\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\right).\dfrac{\sqrt{x}-2}{\sqrt{x}}\left(dkxd:x>0,x\ne4\right)\)
\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+2}.\sqrt{x}\)
\(=\dfrac{2}{\sqrt{x}+2}\)
a: \(A=\dfrac{\sqrt{a}+1+a-\sqrt{a}}{\left(\sqrt{a}+1\right)\cdot\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}\)
\(=\dfrac{\left(a+1\right)\left(\sqrt{a}-1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\)
b: \(B=\dfrac{3\sqrt{x}-3-\sqrt{x}-1-\sqrt{x}+3}{x-1}=\dfrac{\sqrt{x}-1}{x-1}\)
=1/(căn x+1)
c: \(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{x-4}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{2\sqrt{x}}{\sqrt{x}}\cdot\dfrac{1}{\sqrt{x}+2}=\dfrac{2}{\sqrt{x}+2}\)