Câu 1 đặt vào hai đầu dây dẫn R1 và R2 một hiệu điện thế U a)biết cường độ dòng điện qua mạch lần lượt là 0,6A và 1,2A.So sánh điện trở R1 và R2 b)biết U=3,6V.Hãy tính R1 và R2 Câu 2 hiệu điện thế giữa hai đầu dây dẫn là 10V , cường độ dòng điện dây dẫn là 0,2A.nếu hiệu điện thế giữa hai đầu dây dẫn trên giảm 2V.hỏi cường độ dòng điện qua dây dẫn đó thay đổi như thế nào? Tôi đang cần gấp mong mọi người giúp ạ!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định luật Ôm, cường độ dòng điện qua các điện trở được tính theo công thức:
I1=U1/R1=2U2/R1
I2=U2/R2=U2/(2R1)
suy ra I1/I2=4 suy ra I1=4I2
⇒ Cường độ dòng điện qua R1 lớn hơn qua R2 4 lần ⇒ Hai bạn đều sai
\(\text{Theo định luật ôm: }\\ I_1=\frac{U_1}{R_1}=\frac{2U_2}{R_1}\\ I_2=\frac{U_2}{R_2}=\frac{U_2}{2R_1}\\ \text{Nên: } \frac{I_1}{I_2} \Rightarrow \frac{I_1}{4I_2}\\ \Rightarrow \text { Cường độ dòng điện qua R1 lớn hơn qua R2 là 4 lần}\\ \text{Nên 2 bạn sai hết}\)

\(I_1=\dfrac{U}{R_1}=\dfrac{16}{R_1}\left(A\right)\)
\(I_2=\dfrac{U}{R_2}=\dfrac{16}{R_2}\left(A\right)\)
\(TC:\)
\(R_1=3R_2\)
\(I_2=I_1+8\)
\(\Leftrightarrow\dfrac{16}{R_2}=\dfrac{16}{R_1}+8\)
\(\Leftrightarrow\dfrac{16}{R_2}=\dfrac{16}{3R_2}+8\)
\(\Leftrightarrow R_2=\dfrac{4}{3}\)Ω
\(R_1=3R_2=3\cdot\dfrac{4}{3}=4\)Ω
\(I_1=\dfrac{16}{4}=4\left(A\right)\)
\(I_2=\dfrac{16}{\dfrac{4}{3}}=12\left(A\right)\)
\(I1=\dfrac{16}{R1}\), \(I2=\dfrac{16}{R2}\)
mà \(R1=3R2=>I1=\dfrac{16}{3R2}\)(1)\(I2=I1+8=>I1+8=\dfrac{16}{R2}=>I1=\dfrac{16}{R2}-8\)(2)
(1)(2)=>\(\dfrac{16}{3R2}=\dfrac{16}{R2}-8< =>R2=\dfrac{4}{3}\)ôm
\(=>R1=4\) ôm
\(=>I1=\dfrac{16}{4}=4\left(A\right)\), \(I2=16:\dfrac{4}{3}=12A\)

Bài 1.
\(R_{tđ}=\dfrac{U}{I}=\dfrac{75}{2,5}=30\Omega\)
Có \(R_1ntR_2\Rightarrow R_1+R_2=30\) \(\Rightarrow2R_2+R_2=30\Rightarrow R_2=10\Omega\)
\(\Rightarrow R_1=30-R_2=30-10=20\Omega\)
BÀI 2.
Ta có: \(R_{tđ}=\dfrac{U}{I}=\dfrac{45}{2,5}=18\Omega\)
Mà \(R_1//R_2\) \(\Rightarrow\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\)
Lại có: \(R_1=\dfrac{3}{2}R_2\)
\(\Rightarrow\dfrac{1}{R}=\dfrac{1}{\dfrac{3}{2}R_2}+\dfrac{1}{R_2}=\dfrac{1}{18}\) \(\Rightarrow R_2=30\Omega\)

Ta có:
\(I_1=\dfrac{U}{R_1}=\dfrac{16}{R_1}\)
\(I_2=\dfrac{U}{R_2}=\dfrac{16}{R_2}\)
Mà theo bài cho:
\(R_1=4R_2\Rightarrow R_2=\dfrac{R_1}{4}\)
\(I_2=I_1+6\) \(\Rightarrow I_1+6=\dfrac{4.16}{R_1}\)
\(\Rightarrow\dfrac{16}{R_1}+6=\dfrac{64}{R_1}\)
\(\Rightarrow\dfrac{48}{R_1}=6\Rightarrow R_1=8\left(\Omega\right)\)
\(\Rightarrow R_2=2\left(\Omega\right)\)
Cường độ dòng điện qua 2 điện trở lần lượt là:
\(I_1=\dfrac{16}{8}=2\) (A)
\(I_2=\dfrac{16}{2}=8\) (A)

Đáp án D
Điện trở mạch mắc nối tiếp R n t = R 1 + R 2 = 3 R 1 .
V ậ y U = 0 , 2 . 3 R 1 = 0 , 6 . R 1
Điện trở mạch mắc song song
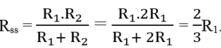
Vậy cường độ dòng điện: I = U/R = 0,9A.

Điện trở mạch mắc nối tiếp: Rnt = R1 + R2 = 3R1
Vậy U = 0,2.3R1 = 0,6R1
Điện trở mạch mắc song song: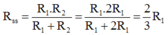
Vậy cường độ dòng điện 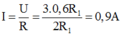
→ Đáp án D

a) Hiệu điện thế U:
\(U=U_1=U_2=U_3=I_1.R_1=0,5.12=6\left(V\right)\)
b) Cường độ dòng điện qua R2:
\(I_2=\dfrac{U_2}{R_2}=\dfrac{6}{10}=0,6\left(A\right)\)
Cường độ dòng điện qua R3:
\(I_3=\dfrac{U_3}{R_3}=\dfrac{15}{6}=2,5\left(A\right)\)
Cường độ dòng điện qua mạch chính:
\(I=I_1+I_2+I_3=0,5+0,6+2,5=3,6\left(A\right)\)
Câu 1:
a) Ta có công thức tính điện trở của \(R_1 ,R_2\) lần lượt là:
\(R_1=\dfrac{U}{I_1}\) và \(R_2=\dfrac{U}{I_2}\)
Theo đề thì ta có: \(I_1< I_2\left(0,6< 1,2\right)\)
Từ đây \(\Rightarrow R_1=\dfrac{U}{I_1}>R_2=\dfrac{U}{I_2}\)
b) Điện trở \(R_1\):
\(R_1=\dfrac{U}{I_1}=\dfrac{3,6}{0,6}=6\Omega\)
Điện trở \(R_2\):
\(R_2=\dfrac{U}{I_2}=\dfrac{3,6}{1,2}=3\Omega\)
Câu 2: Điện trở giữa hai đầu dây dẫn là:
\(R=\dfrac{U_1}{I_1}=\dfrac{10}{0,2}=50\Omega\)
Hiệu điện thế sau khi thay đổi:
\(U_2=10-2=8V\)
⇒ Cường độ dòng điện thay đổi:
\(I_2=\dfrac{U_2}{R}=\dfrac{8}{50}=\dfrac{4}{25}A\)