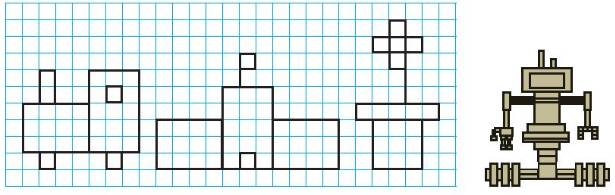
Vẽ một hình mà em thích từ những hình vuông hoặc hình chữ nhật (theo mẫu)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ML
1
CM
17 tháng 11 2018
Diện tích hình vuông ABCD là:
4 × 4 = 16 ( cm 2 )
Diện tích của hình chữ nhật MNOP là:
5 × 2 = 10 ( cm 2 )
Vì 16 cm 2 > 10 cm 2 nên cần dùng cụm từ “lớn hơn” để điền vào chỗ trống.
ML
2
QT
Quoc Tran Anh Le
Giáo viên
8 tháng 12 2023
Học sinh tự gấp rồi cắt tờ giấy hình chữ nhật thành một hình vuông và một hình chữ nhật theo mẫu đã cho.
2 tháng 6 2023
Ta có : 53 x 53 = 2809
=> S(HCN) > 2809 m2
Mà 2809 : 50 = 56 ( dư 9)
=> Chiều rộng hình chữ nhật lúc sau lớn hơn 56 và nhỏ hơn 60 ( vì 60 - 10 = 50- vô lí)
=> S( HCN ) > 50 × 56 = 2800m2 và < 50 × 60 = 3000 m2.
Từ đó => S(HCN) = 2916 m2 (vì chỉ có 54 x 54 = 2916 nằm trong khoảng trên)
=> Chiều rộng hình chữ nhật là 2916 : 50 - 10 = 48,32 m
CM
19 tháng 5 2017
Đổi 1 , 35 d m = 13 , 5 c m
Chu vi hình vuông ABCD là: 9 , 56 × 4 = 38 , 24 ( c m )
Chu vi hình chữ nhật MNPQ là:
( 13 , 5 + 8 , 75 ) × 2 = 44 , 5 ( c m )
Mà 38 , 24 c m < 44 , 5 c m
Vậy chu vi hình vuông ABCD nhỏ hơn chu vi hình chữ nhật MNPQ.
Đáp án A
NL
21 tháng 4 2017
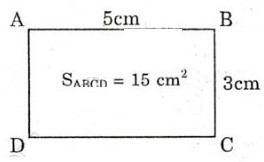
a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2).
- Hình chữ nhật có kích thước 1cm x 12cm có diện tích là 12cm2 và chu vi là ( 1+12).2 = 26(cm) (có 26>15).
- Hình chữ nhật có kích thước 2cmx7cm co diện tích là 14cm2 và chu vi là (2+7).2 = 18(cm) (có 18 > 15).
Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.
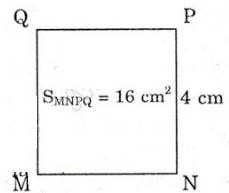
b) Chu vi hình chữ nhật ABCD đã cho là:
(5+3).2 = 16 (cm)
Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là:
16:4 = 4(cm).
Diện tích hình vuông này là 4.4 = 16 (m2)
Vậy Shcn < Shv
Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tich lớn nhất.
Ta luôn có 
≥ √ab
Suy ra ab ≤ .
Hình trên là hình vẽ chứng tỏ hình chữ nhật cạnh a,b (a>b) có diện tích nhỏ hơn diện tích hình vuông cạnh .
Trên hình a= 5cm, b = 3cm, = 4cm
a - = 1cm, - b = 1cm
Do đó
SEBCG = b. ( a- ) = 3.1 = 3 (cm2).
SDGHI = . ( - b ) = 4.1 = 4 (cm2).
SAEGD = b. = 3.4 = 12 (cm2).
Nên SABCD = SEBCG + SAEGD = 3 + 12 = 15(cm2).
SAEHI = SDGHI + SAEGD = 4 + 12 = 16 (cm2).
Vậy SABCD < SAEHI
Tổng quát:
Hình chữ nhật EBCG có một cạnh bằng a - , cạnh kia bằng b.
Hình chữ nhật DGHI có một cạnh bằng - b, cạnh kia bằng .
Mà a - bằng - b và b < ( theo giả thiết a> b)
nên SEBCG < SDGHI
Cộng thêm SAEGD vào mỗi vế bất đẳng thức ta được
SEBCG + SAEGD < SDGHI + SAEGD
Vậy SABCD < SAEHI
21 tháng 4 2017
Hướng dẫn giải:
a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2).
- Hình chữ nhật có kích thước 1cm x 12cm có diện tích là 12cm2 và chu vi là ( 1+12).2 = 26(cm) (có 26>15).
- Hình chữ nhật có kích thước 2cmx7cm co diện tích là 14cm2 và chu vi là (2+7).2 = 18(cm) (có 18 > 15).
Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.
b) Chu vi hình chữ nhật ABCD đã cho là:
(5+3).2 = 16 (cm)
Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là:
16:4 = 4(cm).
Diện tích hình vuông này là 4.4 = 16 (m2)
Vậy Shcn < Shv
Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tich lớn nhất.
Ta luôn có ≥ √ab
Suy ra ab ≤ .
Hình trên là hình vẽ chứng tỏ hình chữ nhật cạnh a,b (a>b) có diện tích nhỏ hơn diện tích hình vuông cạnh .
Trên hình a= 5cm, b = 3cm, = 4cm
a - = 1cm, - b = 1cm
Do đó
SEBCG = b. ( a- ) = 3.1 = 3 (cm2).
SDGHI = . ( - b ) = 4.1 = 4 (cm2).
SAEGD = b. = 3.4 = 12 (cm2).
Nên SABCD = SEBCG + SAEGD = 3 + 12 = 15(cm2).
SAEHI = SDGHI + SAEGD = 4 + 12 = 16 (cm2).
Vậy SABCD < SAEHI
Tổng quát:
Hình chữ nhật EBCG có một cạnh bằng a - , cạnh kia bằng b.
Hình chữ nhật DGHI có một cạnh bằng - b, cạnh kia bằng .
Mà a - bằng - b và b < ( theo giả thiết a> b)
nên SEBCG < SDGHI
Cộng thêm SAEGD vào mỗi vế bất đẳng thức ta được
SEBCG + SAEGD < SDGHI + SAEGD
Vậy SABCD < SAEHI
CM
1 tháng 5 2018
Đáp án B
Lưới hình vuông ở trên được tạo thành bởi 7 đường kẻ dọc và 5 đường kẻ ngang. Với mỗi cách chọn hai đường kẻ ngang và hai đường kẻ dọc ta thu được đúng một hình chữ nhật với các đỉnh là giao điểm của các đường đó. Từ đó suy ra số hình chữ nhật cần tìm là:
C 7 2 . C 5 2 = 210 .
Học sinh tự làm.