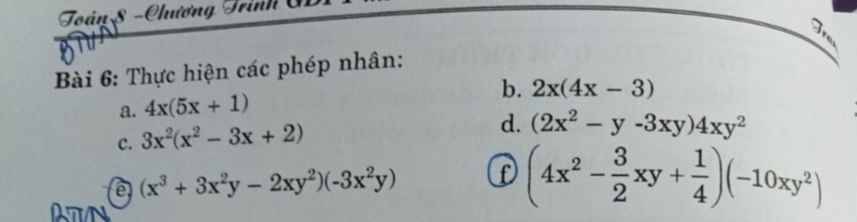 giúp e cậu e, f vs ạ
giúp e cậu e, f vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(f\left(x\right)-g\left(x\right)\)
\(=\left(10x^7-8x^5-6x^3+4x+\dfrac{1}{4}\right)-\left(9x^8-7x^6-5x^4+3x^2+\dfrac{3}{4}\right)\)
\(=10x^7-8x^5-6x^3+4x+\dfrac{1}{4}-9x^8+7x^6+5x^4-3x^2-\dfrac{3}{4}\)
\(=-9x^8+10x^7+7x^6-8x^5+5x^4-6x^3-3x^2+4x+\left(\dfrac{1}{4}-\dfrac{3}{4}\right)\)
\(=-9x^8+10x^7+7x^6-8x^5+5x^4-6x^3-3x^2+4x-\dfrac{1}{2}\)

\(f,f\left(x\right)⋮g\left(x\right)\\ \Leftrightarrow4x^4-13x^3+23x^2+18x-k=\left(x+4\right)\cdot c\left(x\right)\)
Thay \(x=-4\left(\text{Bổ đề Bézout}\right)\)
\(\Leftrightarrow4\cdot\left(-4\right)^4-13\cdot\left(-4\right)^3+23\cdot\left(-4\right)^2+18\left(-4\right)-k=0\\ \Leftrightarrow1024+832+368-72-k=0\\ \Leftrightarrow k=2152\)
\(d,f\left(x\right)⋮g\left(x\right)\\ \Leftrightarrow x^4-8x^3+24x^2+7x+k=\left(x+4\right)\cdot a\left(x\right)\)
Thay \(x=-4\left(\text{Bổ đề Bézout}\right)\)
\(\Leftrightarrow\left(-4\right)^4-8\left(-4\right)^3+24\left(-4\right)^2+7\left(-4\right)+k=0\\ \Leftrightarrow256+512+384-28+k=0\\ \Leftrightarrow k=-1124\)

\(e,\left(x-2\right)^2-16=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\\ f,x^2-5x-14=0\\ \Leftrightarrow\left(x-7\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ g,8x\left(x-3\right)+x-3=0\\ \Leftrightarrow\left(8x+1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{8}\\x=3\end{matrix}\right.\)

\(21,\\ e,PT\Leftrightarrow\left|2x-5\right|=5-2x\Leftrightarrow\left[{}\begin{matrix}2x-5=5-2x\left(x\ge\dfrac{5}{2}\right)\\5-2x=5-2x\left(x< \dfrac{5}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(tm\right)\\0x=0\left(tm\right)\end{matrix}\right.\\ \Leftrightarrow x\in R\\ f,\Leftrightarrow\left|x-\dfrac{1}{4}\right|=\dfrac{1}{4}-x\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{4}=\dfrac{1}{4}-x\left(x\ge\dfrac{1}{4}\right)\\\dfrac{1}{4}-x=\dfrac{1}{4}-x\left(x< \dfrac{1}{4}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\left(tm\right)\\0x=0\left(tm\right)\end{matrix}\right.\\ \Leftrightarrow x\in R\)

\(f\left(0\right)=2010\Rightarrow a.0^2+b.0+c=2010\Rightarrow c=2010\)
\(f\left(1\right)=2011\Rightarrow a.1^2+b.1+c=2011\Rightarrow a+b+c=2011\)
\(\Rightarrow a+b+2010=2011\Rightarrow a+b=1\) (1)
\(f\left(-1\right)=2012\Rightarrow a.\left(-1\right)^2+b.\left(-1\right)+c=2012\)
\(\Rightarrow a-b+c=2012\Rightarrow a-b+2010=2012\)
\(\Rightarrow a-b=2\Rightarrow a=b+2\)
Thế vào (1) \(\Rightarrow b+2+b=1\Rightarrow2b=-1\Rightarrow b=-\dfrac{1}{2}\)
\(\Rightarrow a=b+2=-\dfrac{1}{2}+2=\dfrac{3}{2}\)
\(\Rightarrow f\left(x\right)=\dfrac{3}{2}x^2-\dfrac{1}{2}x+2010\)
\(\Rightarrow f\left(-2\right)=\dfrac{3}{2}.\left(-2\right)^2-\dfrac{1}{2}.\left(-2\right)+2010=2017\)

Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)

g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)

a: CH=16^2/24=256/24=32/3(cm)
BC=24+32/3=104/3cm
AC=căn 32/3*104/3=16/3*căn 13(cm)
b: BC=12^2/6=144/6=24cm
CH=24-6=18cm
AC=căn 18*24=12*căn 3(cm)
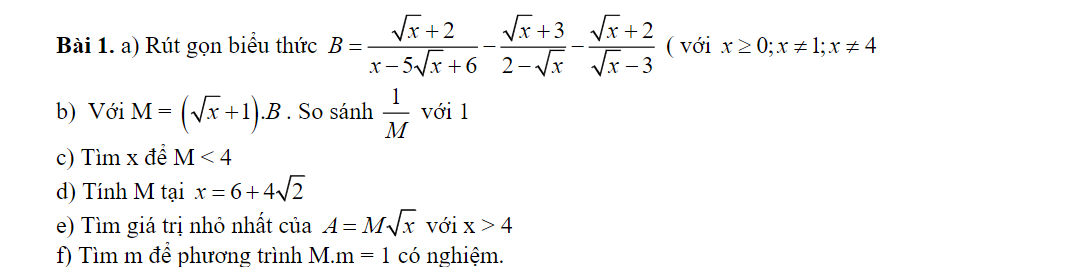 câu e và f cần giúp đỡ vs ạ
câu e và f cần giúp đỡ vs ạ 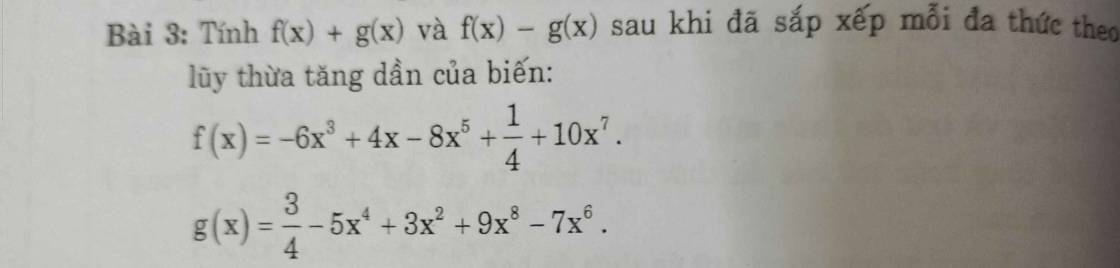






\(e,\left(x^3+3x^2y-2xy^2\right)\left(-3x^2y\right)\)
\(=\left(-3x^2.x^3.y\right)+\left(-3x^2y.3x^2y\right)+\left(-3x^2y.\left(-2xy^2\right)\right)\)
\(=-3x^5y-9x^4y^2+6x^3y^3\)
\(f,\left(4x^2-\dfrac{3}{2}xy+\dfrac{1}{4}\right)\left(-10xy^2\right)\)
\(=\left(-10xy^2.4x^2\right)+\left(-10xy^2.\left(-\dfrac{3}{2}xy\right)\right)+\left(-10xy^2.\dfrac{1}{4}\right)\)
\(=-40x^3y^2+15x^2y^3-\dfrac{5}{2}xy^2\)
Em cảm ơn ạ 💞