Giúp em mấy bài đánh dấu với ạ😭
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\overrightarrow{AB}=\left(-4;3\right)AC;=\left(-2;0\right)\)
Vì -2/-4<>0/3
nên A,B,C không thẳng hàng
=>A,B,C là ba đỉnh của một tam giác
b: A là trung điểm của EC
=>\(\left\{{}\begin{matrix}x_E+1=2\cdot3=6\\y_E-1=2\cdot\left(-1\right)=-2\end{matrix}\right.\Leftrightarrow E\left(5;-1\right)\)
c: A là trọng tâm của tam giác BCG
=>\(\left\{{}\begin{matrix}-1+1+x_G=3\cdot3=9\\2-1+y_G=3\cdot\left(-1\right)=-3\end{matrix}\right.\Leftrightarrow G\left(9;-4\right)\)
d: ADBC là hình bình hành
=>vecto AD=vecto CB
vecto CB=(-2;3)
vecto AD=(x-3;y+1)
Do đó, ta có:
x-3=-2 và y+1=3
=>x=1 và y=2
=>D(1;2)
f: Tọa độ H là;
\(\left\{{}\begin{matrix}x=\dfrac{3-1+1}{3}=1\\y=\dfrac{-1+2-1}{3}=0\end{matrix}\right.\)

Giả sử đường thẳng chắn trên hai trục tọa độ 2 đoạn bằng nhau bằng a \(\left(a\ne0\right)\)
Khi đó, tọa độ giao điểm là: (a;0), (0;a)
Phương trình đường thẳng là: \(\dfrac{x-a}{a-0}=\dfrac{y-0}{0-a}\Leftrightarrow-a\left(x-a\right)=ay\)
\(\Leftrightarrow-x+a=y\) (*)
a. Thay M(-4;10) vào (*) ta được: \(-\left(-4\right)+a=10\Rightarrow a=6\)
Phương trình đường thẳng cần tìm là: y=-x+6
b. Thay M(2;1) vào (*) ta được: \(-2+a=1\Rightarrow a=3\)
Phương trình đường thẳng cần tìm là: y=-x+3

5:
a: sin x=2*cosx
\(A=\dfrac{6cosx+2cosx-4\cdot8\cdot cos^3x}{cos^3x-2cosx}\)
\(=\dfrac{8-32cos^2x}{cos^2x-2}\)
b: VT=sin^4(pi/2-x)+cos^4(x+pi/2)+6*1/2*sin^22x+1/2*cos4x
=cos^4x+sin^4x+3*sin^2(2x)+1/2*(1-2*sin^2(2x))
=1-2*sin^2x*cos^2x+3*sin^2(2x)+1/2-sin^2(2x)
==3/2=VP

9: Ta có: \(\left(1+\sqrt{2}-\sqrt{3}\right)\left(1+\sqrt{2}+\sqrt{3}\right)\)
\(=\left(\sqrt{2}+1\right)^2-3\)
\(=3+2\sqrt{2}-3=2\sqrt{2}\)
10: Ta có: \(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{6}-\sqrt{2}}+2\sqrt{10}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{2}\left(\sqrt{3}-1\right)}+2\sqrt{10}\)
\(=\dfrac{\sqrt{10}}{2}+\dfrac{4\sqrt{10}}{2}=\dfrac{5\sqrt{10}}{2}\)
13)\(\dfrac{2\sqrt{10}+\sqrt{30}-2\sqrt{2}-\sqrt{6}}{2\sqrt{10}-2\sqrt{2}}=\dfrac{\sqrt{10}\left(2+\sqrt{3}\right)-\sqrt{2}\left(2+\sqrt{3}\right)}{2\left(\sqrt{10}-\sqrt{2}\right)}\)\(=\dfrac{\left(\sqrt{10}-\sqrt{2}\right)\left(2+\sqrt{3}\right)}{2\left(\sqrt{10}-\sqrt{2}\right)}=\dfrac{2+\sqrt{3}}{2}\)
14)sai đề? phải là \(\sqrt{3-\sqrt{5}}\)
\(=\dfrac{\sqrt{3-\sqrt{5}}\left(3+\sqrt{5}\right)}{2\sqrt{10}-2\sqrt{2}}=\dfrac{\sqrt{6-2\sqrt{5}}\left(3+\sqrt{5}\right)}{\sqrt{2}\left(2\sqrt{10}-2\sqrt{2}\right)}\)
\(=\dfrac{\sqrt{\left(\sqrt{5}-1\right)^2}\left(3+\sqrt{5}\right)}{4\left(\sqrt{5}-1\right)}=\dfrac{\left|\sqrt{5}-1\right|\left(3+\sqrt{5}\right)}{4\left(\sqrt{5}-1\right)}\)
\(=\dfrac{3+\sqrt{5}}{4}\)
15)\(\sqrt{\left(1-\sqrt{2016}\right)^2}.\sqrt{2017+2\sqrt{2016}}=\left|1-\sqrt{2016}\right|\sqrt{1+2\sqrt{2016}+2016}\)
\(=\left(\sqrt{2016}-1\right)\sqrt{\left(1+\sqrt{2016}\right)^2}=\left(\sqrt{2016}-1\right)\left(1+\sqrt{2016}\right)\)
\(=2015\)





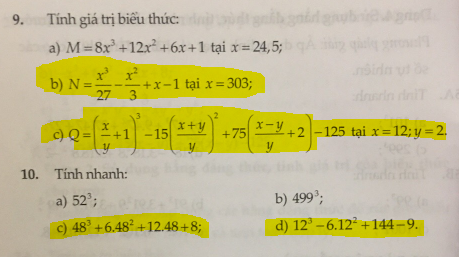 Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người.
Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người. 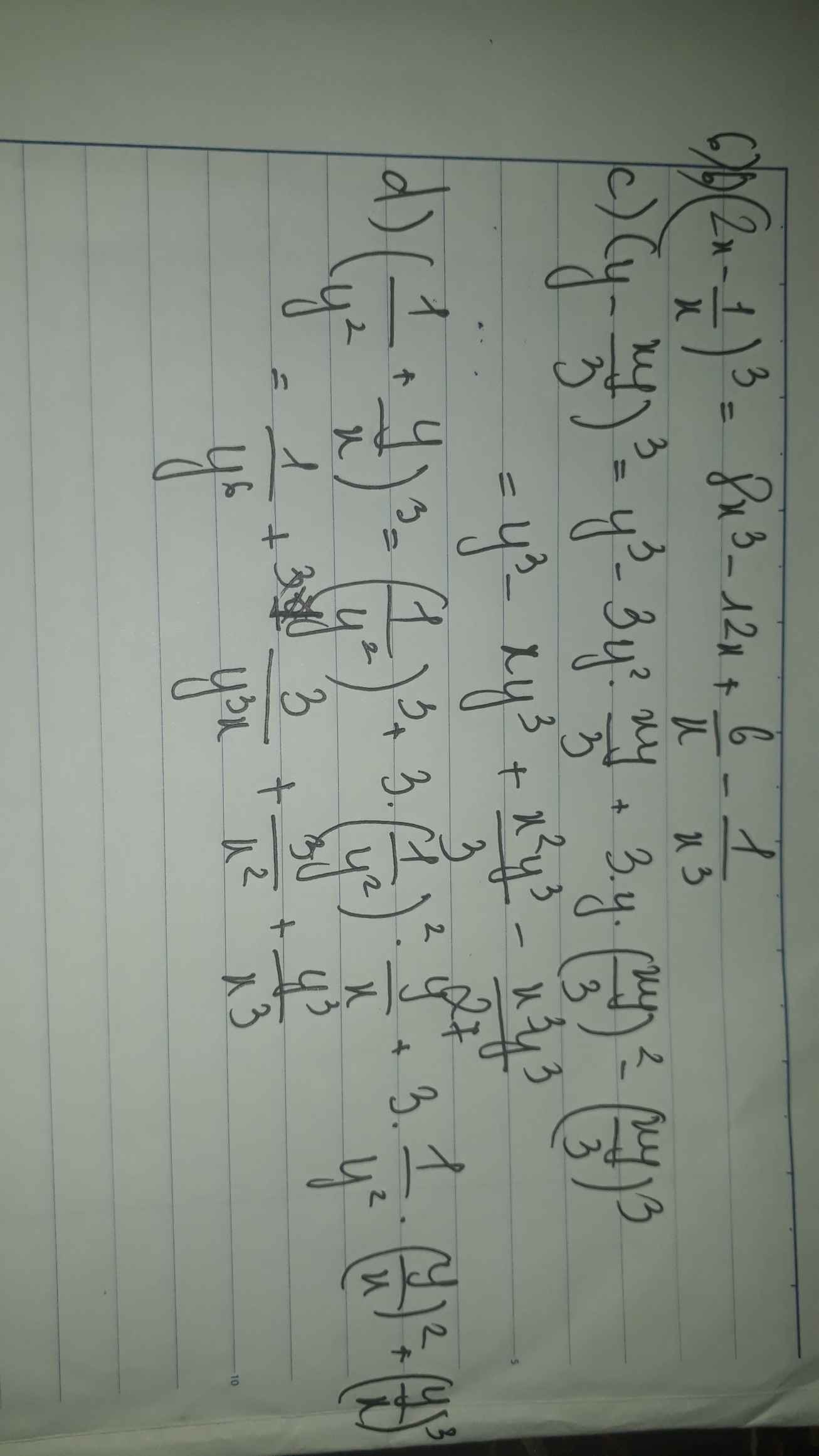
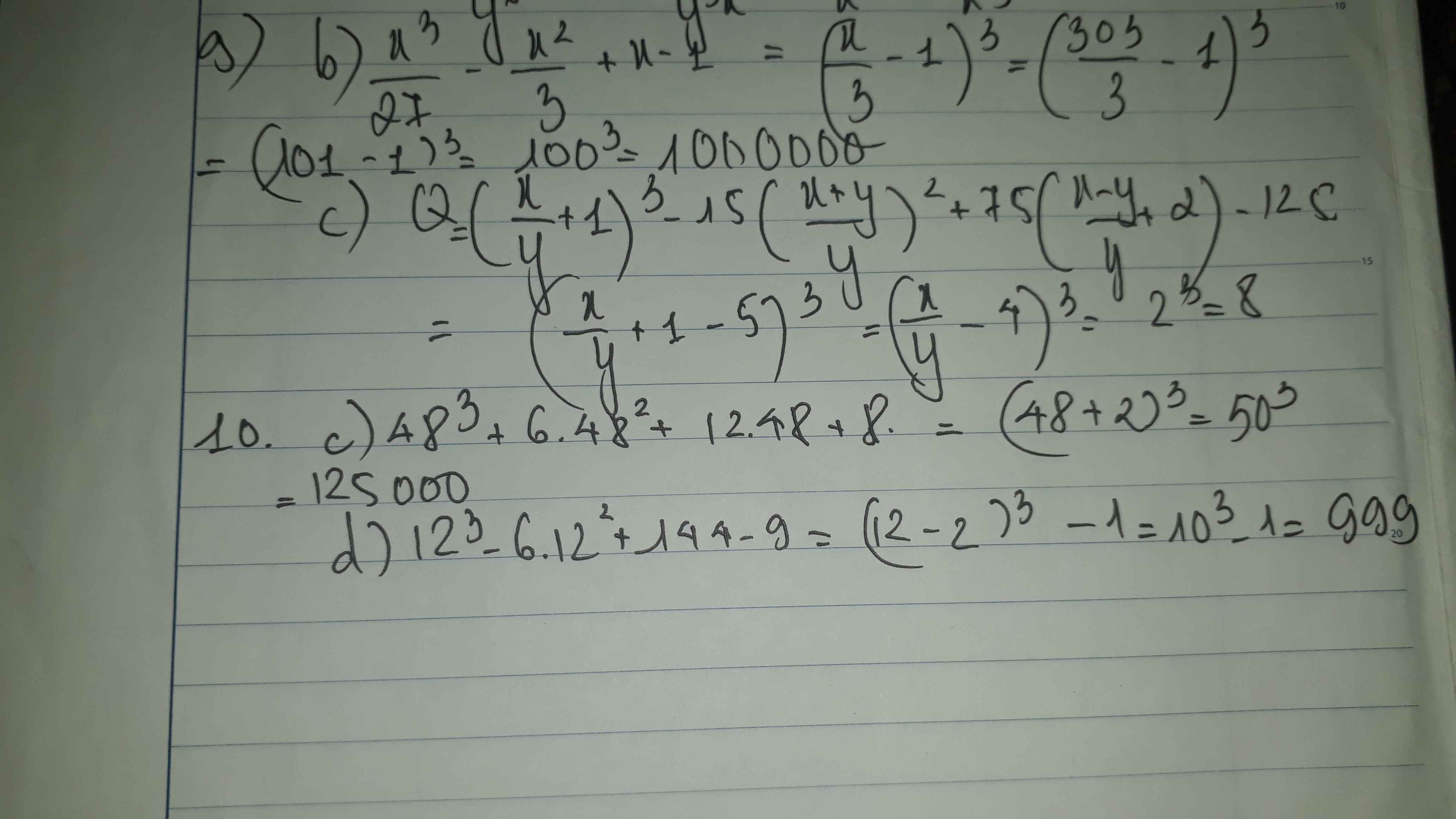



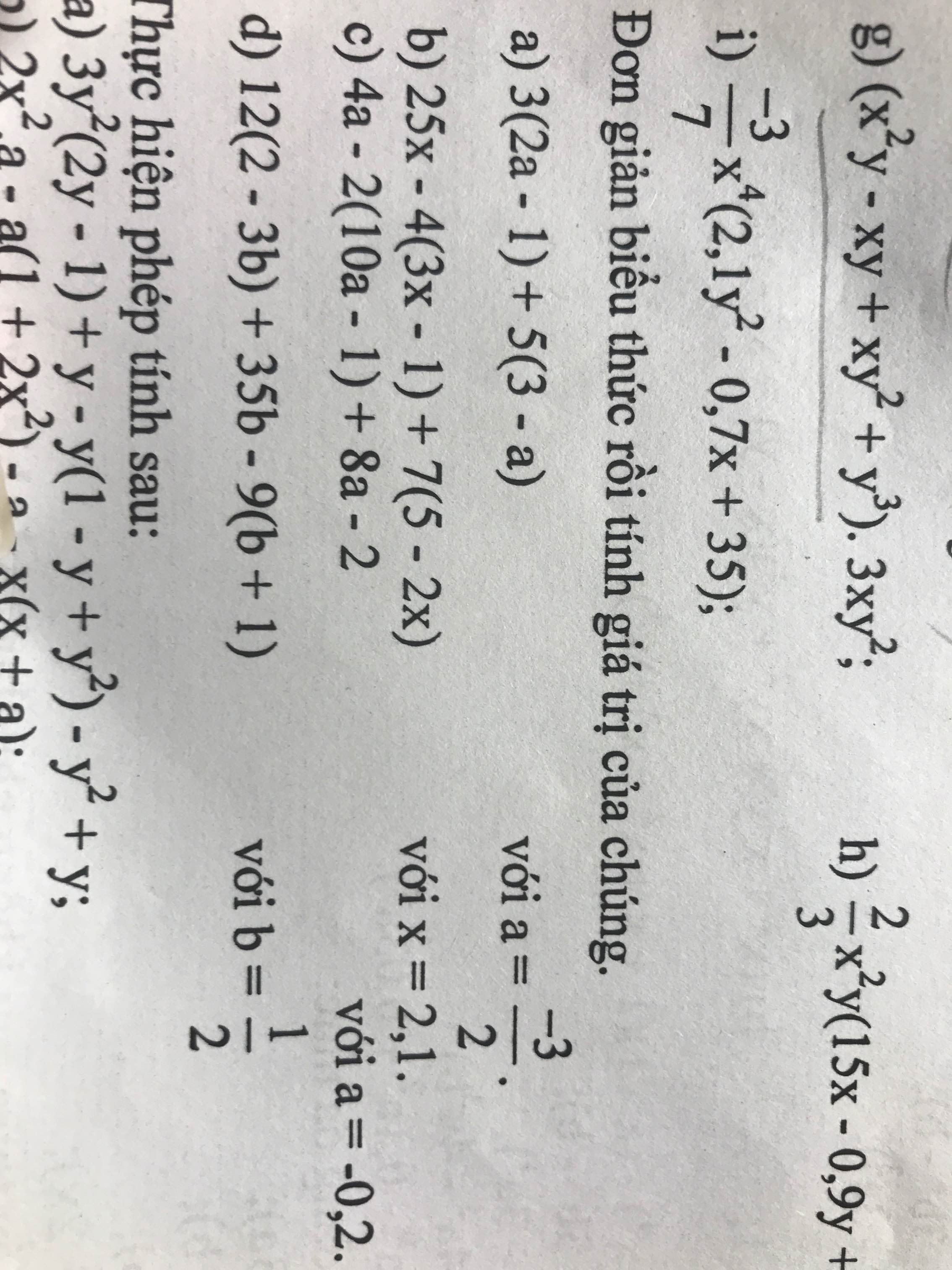




10:
a: A=(2^2-1)(2^2+1)*...*(2^16+1)
=(2^4-1)(2^4+1)(2^8+1)(2^16+1)
=(2^8-1)(2^8+1)(2^16+1)
=(2^16-1)(2^16+1)
=2^32-1
b: B=(127+73)^2=200^2=40000
c: C=18^8-18^8+1=1
d: D=560*1000/200^2=14