Cho hình vuông ABCD có cạnh = 12.Tính diện tích hình AECF. Biết DE=EF=FB.
A B D C E F
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) S hình vuông ABCD: 12x12=144 cm2
b) Ta có sơ đồ hình vuông ABCD cạnh 12 cm. Lấy điểm e và f sao cho be=ef=fd. Khi nối các điểm a,e,c,f thì ta đc hình thang AECF.
Độ dài đáy bé của hình thang AECF: 12:3=4 cm
S hình thang AECF: (12+4)x12:2= 96 cm2
Đáp số: a) 144cm2
b) 96cm2

Xét ba tam giác ADF,AFE,AEB có:chung chiều cao hạ từ đỉnh A xuống DB có đáy DF=FE=EB
=>SADF=SFAE=SAEB
=>SFAE=1/3 x SADB
Xét 3 tam giác CDF,FCE,CEB có chung chiều cao hạ từ đỉnh C xuống BD đáy DF=FE=EB
=>SDFE=SFCE=SCEB
=>SFCE=1/3 x SDCB
Ta có: SAECF=SFAE+SFCE=1/3x SADB+1/3 x SDCB=1/3x(SADB+SDCB)=1/3 x SABCD=1/3 x12 x12=48 (cm2)
Tick cho mình nha Đỗ Vân Nhi

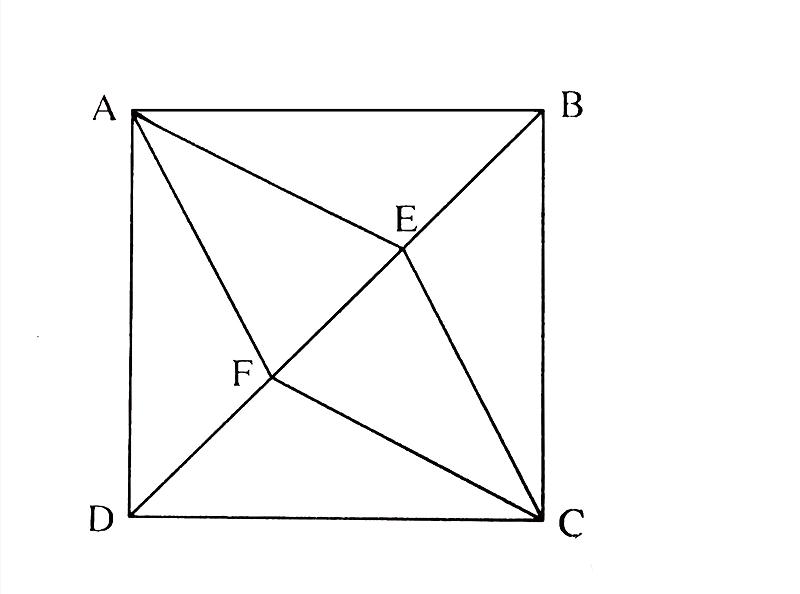
Ta có: △ ADF ; △ AFE ; △ AEB có chung chiều cao, hạ từ đỉnh A xuống DB, có đáy DF = FE = EB ⇒ \(S_{ADF}=S_{AFE}=S_{AEB}\)
⇒ \(S_{AFE}=\dfrac{1}{3}S_{ADB}\)
Ta lại có: △ CDF ; △ FCE ; △ CEB có chung chiều cao, hạ từ đỉnh C xuống DB, có đáy DF = FE = EB ⇒ \(S_{CDF}=S_{FCE}=S_{CEB}\)
⇒ \(S_{FCE}=\dfrac{1}{3}S_{DCB}\)
Vậy \(S_{AECF}=S_{AFE}+S_{FCE}=\dfrac{1}{3}S_{ADB}+\dfrac{1}{3}S_{DCB}\) \(=\dfrac{1}{3}\left(S_{ADB}+S_{DCB}\right)=\dfrac{1}{3}S_{AECF}=\dfrac{1}{3}\times\left(12\times12\right)=48\left(cm^2\right)\)

Mình không biết vẽ hình trên OnlineMath
S AECF là ;
12x12:3=48 (cm2)
Đáp số : 48cm2

tôi ko biết thằng ml này là ai nó gửi lung tung là chết với tôi
Ta có DE = EF = FB, và đoạn BD chia đoạn thẳng DE, EF, FB thành 3 đoạn, mỗi đoạn bằng:
12 : 3 = 4 ( cm )
Kẻ hình thành 2 tam giác là tam giác AEB và tam giác CDF bằng nhau:
Diện tích của tam giác AEB = tam giác CDF là:
4 x 12 : 2 = 24 ( cm2 )
Diện tích của hình vuông ABCD là:
12 x 12 = 144 ( cm2 )
Diện tích của AECF là:
144 - ( 24 x 2 ) = 96 ( cm2 )
Vậy diện tích của AECF là 96 cm2