Ba ông và ba bà ngồi trên một dãy ghế.
1. Tính xác suất để người cùng phái ngồi gần nhau.
2. Tính xác suất để ba bà ngồi gần nhau.
3. Tính xác suất để họ ngồi nam nữ xen kẽ nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
26 tháng 5 2023
Kí hiệu tắt ông là M và bà là W. Không gian mẫu E có \(6!=720\) (phần tử).
1.
Có 2 cách xếp người cùng phái ngồi gần nhau: \(MMMWWW,WWWMMM\).
Có \(3!=6\) cách ngồi của 3 ông và có \(3!=6\) cách ngồi của 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{2.3!.3!}{6!}=\dfrac{1}{10}\)
2.
Có 4 cách sắp xếp 3 bà ngồi gần nhau: \(MMMWWW,MMWWWM,MWWWMM,WWWMMM\).
Có \(3!=6\) cách sắp xếp 3 ông và có \(3!=6\) cách sắp xếp 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{4.3!.3!}{6!}=\dfrac{1}{5}\).
3.
Có 2 cách sắp xếp 3 ông và 3 bà ngồi xen kẽ nhau: \(MWMWMW,WMWMWM.\)
Có \(3!=6\) cách sắp xếp 3 ông và có \(3!=6\) cách sắp xếp 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{2.3!.3!}{6!}=\dfrac{1}{10}\)
CM
7 tháng 8 2017
Không gian mẫu là việc sắp xếp 6 bạn vào 6 ghế tùy ý
⇒ n(Ω) = P6 = 6! = 720.
a. Gọi A: “ Nam, nữ ngồi xen kẽ nhau”
+ Chọn chỗ ngồi cho 3 bạn nữ: Có 2 cách (Vị trí 1,3,5 hoặc 2,4,6).
+ Sắp xếp 3 bạn nữ vào 3 chỗ: Có 3! = 6 cách
+ Sắp xếp 3 bạn nam vào 3 chỗ còn lại: Có 3! = 6 cách
⇒ Theo quy tắc nhân: n(A) = 2.6.6 = 72 (cách).
⇒ n(A) = 2.3!.3! = 72
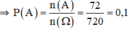
b. B: “Ban bạn nam ngồi cạnh nhau”
+ Chọn 3 chỗ ngồi cạnh nhau cho 3 bạn nam: Có 4 cách.
+ Sắp xếp 3 bạn nam vào 3 chỗ: Có 3! = 6 cách.
+ Sắp xếp 3 bạn nữ vào 3 chỗ còn lại: Có 3! = 6 cách
⇒ Theo quy tắc nhân: n(B) = 4.6.6 = 144 (cách)
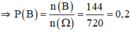
Xác suất để ba bạn nam ngồi cạnh nhau là:
Q
4 tháng 4 2017
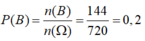
Số cách xếp 3 nam và 3 nữ vào 6 ghế là 6! Cách.
Suy ra: \(n\left(\Omega\right)=6!=720\)
a) Ta gọi A là biến cố : “Nam, nữ ngồi xen kẽ nhau”
Ta đánh số ghế như sau:
| 1 | 2 | 3 | 4 | 5 | 6 |
Trường hợp 1:
+ Nam ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nữ ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Trường hợp 2:
+ Nữ ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nam ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Suy ra:
N(A) = 3!.3! + 3!.3! = 36 + 36 = 72 cách xếp.
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{72}{720}=\dfrac{1}{10}=0,1\)
b) Gọi biến cố B: “Ba bạn nam ngồi cạnh nhau”
Xem 3 bạn nam như một phần tử N và N cùng 3 bạn nữ được xem như ngồi vào 4 ghế được đánh số như sau:
| 1 | 2 | 3 | 4 |
_ Số cách xếp N và 3 nữ vào 4 ghế là 4!
_ Mỗi cách hoán vị 3 nam cho nhau trong cùng một vị trí ta có thêm 3! cách xếp khác nhau.
Suy ra n(B) = 4!.3!=144
Vậy: \(P\left(B\right)=\dfrac{n\left(B\right)}{n\left(\Omega\right)}=\dfrac{144}{720}=\dfrac{1}{5}=0,2\)
MH
9 tháng 4 2017
Số cách xếp 3 nam và 3 nữ vào 6 ghế là 6! Cách.
Suy ra: n(Ω)=6!=720n(Ω)=6!=720
a) Ta gọi A là biến cố : “Nam, nữ ngồi xen kẽ nhau”
Ta đánh số ghế như sau:
|
1 |
2 |
3 |
4 |
5 |
6 |
Trường hợp 1:
+ Nam ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nữ ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Trường hợp 2:
+ Nữ ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nam ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Suy ra:
N(A) = 3!.3! + 3!.3! = 36 + 36 = 72 cách xếp.
Vậy P(A)=n(A)n(Ω)=72720=110=0,1P(A)=n(A)n(Ω)=72720=110=0,1
b) Gọi biến cố B: “Ba bạn nam ngồi cạnh nhau”
Xem 3 bạn nam như một phần tử N và N cùng 3 bạn nữ được xem như ngồi vào 4 ghế được đánh số như sau:
|
1 |
2 |
3 |
4 |
_ Số cách xếp N và 3 nữ vào 4 ghế là 4!
_ Mỗi cách hoán vị 3 nam cho nhau trong cùng một vị trí ta có thêm 3! cách xếp khác nhau.
Suy ra n(B) = 4!.3!=144
Vậy : P(B)=n(B)n(Ω)=144720=15=0,2
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 1
Không gian mẫu: \(8!\)
Có 2 kiểu xếp (kí hiệu N là nam, n là nữ): \(NnNnNnNn\) hoặc \(nNnNnNnN\)
Hoán vị 4 bạn nữ: \(4!\) cách
Hoán vị 4 bạn nam: \(4!\) cách
\(\Rightarrow2.4!.4!\) cách xếp thỏa mãn
Xác suất...