Cho một tam giác đều 15 cạnh. Chứng minh rằng khi chọn ra 7 điểm bất kỳ trong số 15 điểm trên thì luôn có 3 đỉnh là đỉnh của 1 tam giác cân.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử ΔABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB; AM ≤ AC.
- TH1 : Nếu M ≡ B hoặc M ≡ C (Kí hiệu đọc là trùng với) thì AM = AB = AC.
- TH2 : Nếu M nằm giữa B và C và M ≠ B; M ≠ C.
Kẻ AH ⊥ BC tại H
+ Nếu M ≡ H ⇒ AM ⊥ BC tại M hay AM là đường vuông góc từ A đến BC.
Mà AB, AC là các đường xiên từ A đến đường thẳng BC.
Theo định lí 1 : Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường thẳng vuông góc là đường ngắn nhất.
⇒ AM < AB và AM < AC.
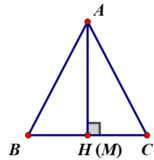
+ Nếu M ≠ H giả sử M nằm giữa H và C ⇒ MH < CH.
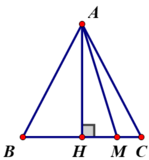
Vì MH và CH lần lượt là hình chiếu của đường xiên MA và CA trên đường BC
Mà MH < CH ⇒ MA < CA (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).
Chứng minh tương tự nếu M nằm giữa H và B
Vậy mọi vị trí của M trên cạnh đáy BC thì AM ≤ AB = AC.

O cách đều 3 đỉnh của tam giác ABC
\( \Rightarrow \) \(OA = OB = OC\)
\( \Rightarrow \) \(\Delta OAB\) cân tại O.
Giả sử O là trung điểm BC
\( \Rightarrow \widehat {OAB} = \widehat {OBA}\)
\(\Delta OAC\) cân tại O
\( \Rightarrow \widehat {OAC} = \widehat {OCA}\)
Xét tam giác ABC có
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\ \Rightarrow \widehat A + \widehat {OAB} + \widehat {OAC} = {180^0}\\ \Rightarrow \widehat A + \widehat A = {180^0}\\ \Rightarrow \widehat A = {90^0}\end{array}\)
Vậy nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.

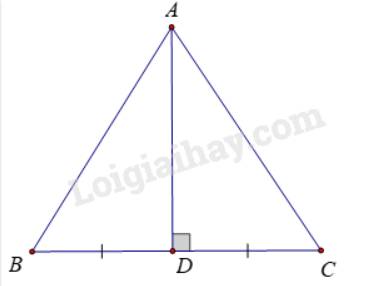
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)
\( \Rightarrow AD\)là đường trung trực của BC.
Xét \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)
\( \Rightarrow \)AD là tia phân giác góc BAC.
Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
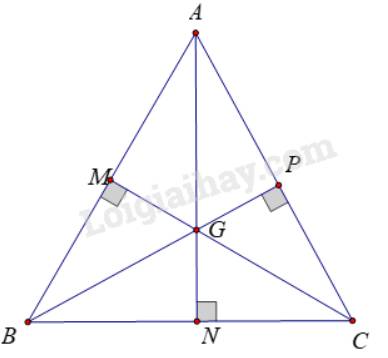
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC
\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất
Sửa đề: Đa giác đều 15 cạnh
=>Tạo ra 3 ngũ giác đều trong đó: Ngũ giác 1 có các đỉnh tô màu đỏ, ngũ giác 2 có các đỉnh tô màu xanh, ngũ giác 3 có các đỉnh tô màu vàng. Ta sẽ xem 3 ngũ giác đó như là 3 khu, 7 điểm ta chọn ra 7 điểm trong đó.
=>7 điểm thuộc vào 3 khu khác nhau thì phải có 1 khu có 3 điểm.
=>Luôn có tam giác cân(3 đỉnh bất kì của một ngũ giác đều tạo thành tam giác cân)