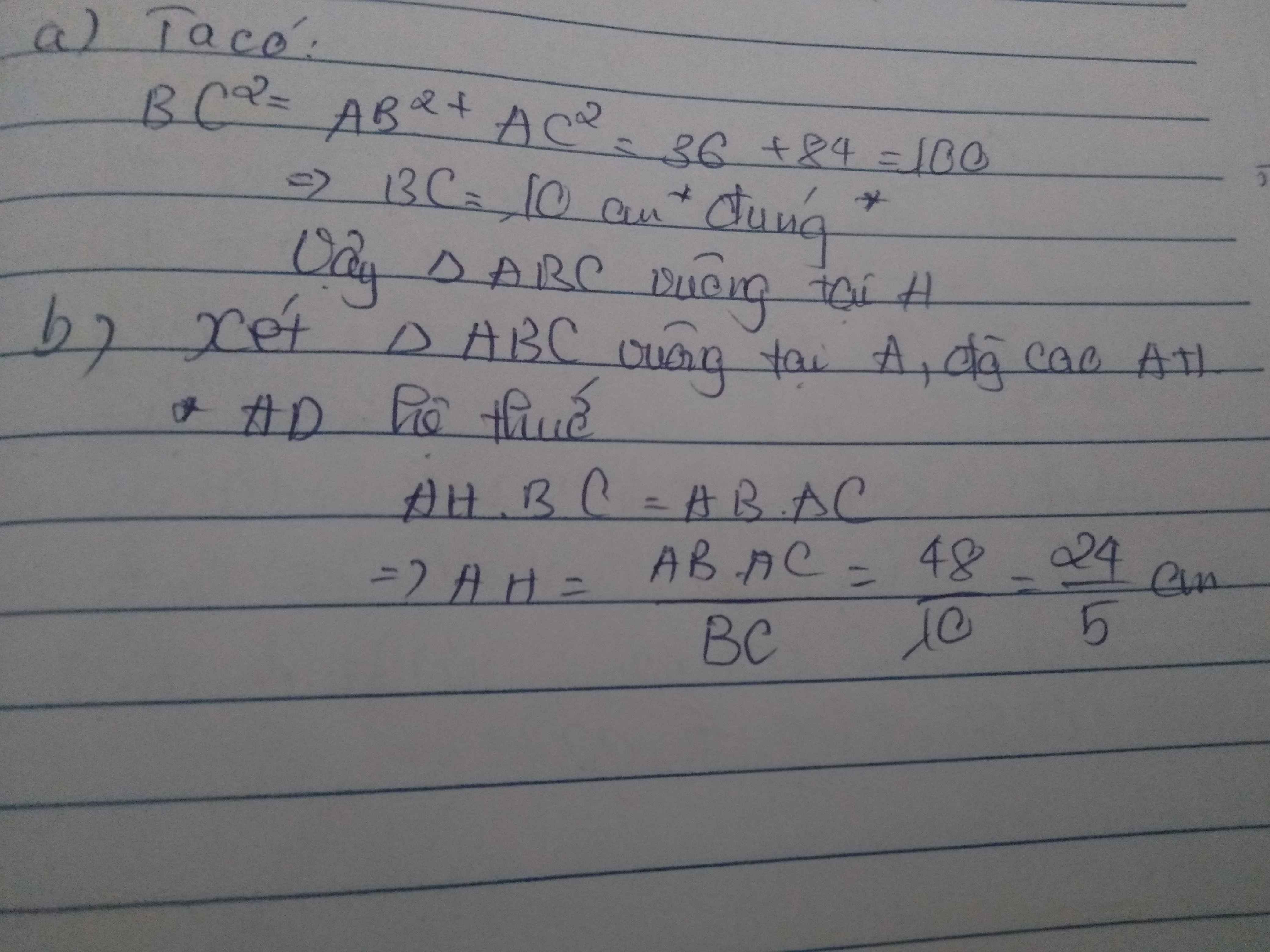giải bài toán: cho tam giác ABC có AB=2cm ;AC=4cm . qua B dựng đường thẳng cắt đoạn AB tại D sao cho góc ABC =góc ACB .chứng minh tam giác ABD đòng dạng với tam giácACB.tÍính độ dàiAD và CD .gọi AH là đường cao của tam giá ABC ,AE là ddường cao của tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
a. Ta có: \(AB^2+AC^2=6^2+8^2=36+64=100\)
\(BC^2=10^2=100\)
\(\Rightarrow AB^2+AC^2=BC^2\) \(\Rightarrow\Delta\)ABC vuông tại A
b. \(\Delta\)ABC vuông tại A, đường cao AH. Ta có:
AB.AC = AH.BC
hay 6.8 = AH.10
=> AH = \(\dfrac{6.8}{10}=4.8\)

Hai tam giác trên có các cạnh tương ứng bằng nhau
có các góc tương ứng bằng nhau
Tam giác ABC và A'B'C' có:
AB = A'B' = 2cm
BC = B'C' = 4 cm
AC = A'C' = 3 cm
=> Tam giác ABC = tam giác A'B'C' (c.c.c)
=> góc A = góc A'
góc B = góc B'
góc C = góc C'

Áp dụng định lý Pi-ta-go ta có:
\(AB^2+AC^2=BC^2\\ \Rightarrow21^2+28^2=BC^2\\ \Rightarrow BC=\sqrt{21^2+28^2}\\ \Rightarrow BC=35\left(cm\right)\)

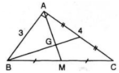
ΔABC vuông tại A có BC2 = AB2 + AC2 (định lí Pitago)
⇒ BC2 = 32 + 42 = 25 ⇒ BC = 5 (cm)
Gọi M là trung điểm của BC ⇒ AM là trung tuyến.
Vì theo đề bài: trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên
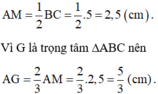

( bạn tự vẽ hình)
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.