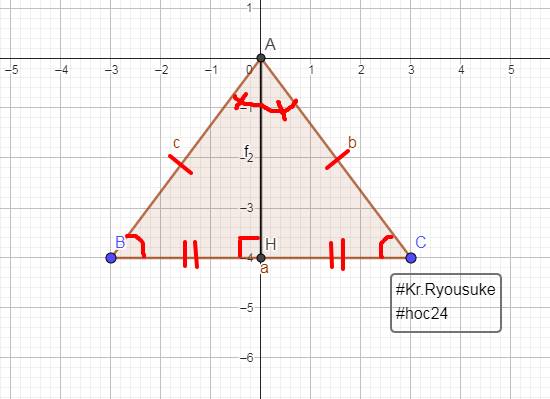
Cho tam giác ABC cân tại A, đường trung tuyến AH
a, chứng minh : tam giác ABH = tam giác ACH
b, chứng minh: AH là đường phân giác của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2023
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta ABH` và `\Delta ACH`:
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
$\widehat {AHB} = \widehat {AHC} (=90^0) (\text {AH là đường cao của} \Delta ABC)$
`=> \Delta ABH = \Delta ACH (ch-gn)`
`b,`
Vì `\Delta ABH = \Delta ACH (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 cạnh tương ứng})$
`-> \text {AH là đường phân giác của}` `\Delta ABC`
`c,`
Vì `\Delta ABH = \Delta ACH (a)`
`-> \text {HB = HC}`
Ta có:
`\text {AH} \bot \text {BC}`
`\text {HB = HC}`
`-> \text {AH là đường trung trực của}` `\Delta ABC`.
12 tháng 5 2023
a: Sửa đề: đường cao AM, cm ΔABM=ΔACM
Xét ΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
=>ΔABM=ΔACM
b: ΔABM=ΔACM
=>MB=MC
=>AM là đường trung tuyến
c: AM=3/2AG=9cm
16 tháng 4 2023
a: Xét ΔAHB và ΔAHC có
AB=AC
góc BAH=góc CAH
AH chung
=>ΔAHB=ΔAHC
b: Xet ΔABC có
AH,BD là trung tuyến
AH cắt BD tại G
=>G là trọng tâm
c: Xét ΔABC có
H là trung điểm của BC
HE//AC
=>E là trung điểm của AB
=>C,G,E thẳng hàng
10 tháng 5 2022
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
DO đó: ΔABH=ΔACH
b: Xét ΔEDH vuông tại D và ΔEDC vuông tại D có
ED chung
HD=CD
Do đó: ΔEDH=ΔEDC
15 tháng 2 2022
a, Xét tam giác ABH và tam giác ACH ta có
AB = AC (gt)
AH _ chung
^AHB = ^AHC = 900
Vậy tam giác ABH = tam giác ACH ( ch - cgv )
b, Xét tam giác ABC cân tại A
AH là đường cao đồng thời là đường trung tuyến
=> H là trung điểm BC
c, Do H là trung điểm BC => HB = 6/2 = 3 cm
Theo định lí Pytago tam giác AHB vuông tại H
\(AH=\sqrt{AB^2-BH^2}=\sqrt{25-9}=4cm\)
18 tháng 7 2021
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔBAC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
b) Xét ΔAMD và ΔCMH có
MA=MC(gt)
\(\widehat{AMD}=\widehat{CMH}\)(hai góc đối đỉnh)
MD=MH(gt)
Do đó: ΔAMD=ΔCMH(c-g-c)
Suy ra: AD=HC(Hai cạnh tương ứng)
c) Ta có: ΔAMD=ΔCMH(cmt)
nên \(\widehat{MAD}=\widehat{MCH}\)(hai góc tương ứng)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//HC(Dấu hiệu nhận biết hai đường thẳng song song)
hay AD//HB
Xét tứ giác ABHD có
AD//BH(cmt)
AD=BH(=HC)
Do đó: ABHD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: AB//DH(Hai cạnh đối)
23 tháng 3 2023
a: Xet ΔABH và ΔACH có
AB=AC
BH=CH
AH chung
=>ΔABH=ΔACH
=>góc BAH=góc CAH
=>AH là phân giác của góc BAC
b: góc DAH=góc CAH=góc DHA
=>ΔDAH cân tại D
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta ABH` và `\Delta ACH`:
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
`\text {HB = HC (AH là đường trung tuyến)}`
`=> \Delta ABH = \Delta ACH (c-g-c)`
`b,`
Vì `\Delta ABH = \Delta ACH (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 góc tương ứng})$
`-> \text {AH là đường phân giác của}` `\Delta ABC`.
ròi AH là cạnh hay góc mà góc chung hay dữ v c :>.