a) Nêu định nghĩa phương trình bậc nhất một ẩn? Lấy 1 ví dụ về phương trình bậc nhất 1 ẩn và xác định các hệ số a,b,c của phương trình đó? b) Viết công thức tính thể tích của hình hộp chữ nhật và giải thích các đại lượng có trong công thức? cm, c) Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 12 cm, AD=16 AA’ = 25 cm. Tính thể tích hình hộp chữ nhật đó. Đang cần gấp lớp 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Phương trình \(7x + \dfrac{4}{7} = 0\) là phương trình bậc nhất một ẩn vì có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số.
Khi đó, \(a = 7;b = \dfrac{4}{7}\).
b) \(\dfrac{3}{2}y - 5 = 4\)
\(\dfrac{3}{2}y - 5 - 4 = 0\)
\(\dfrac{3}{2}y - 9 = 0\)
Phương trình \(\dfrac{3}{2}y - 9 = 0\) là phương trình bậc nhất một ẩn vì có dạng \(ay + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(y\) là ẩn số.
Khi đó, \(a = \dfrac{3}{2};b = - 9\)
c) Phương trình \(0t + 6 = 0\) không là phương trình bậc nhất một ẩn.
Mặc dù phương trình đã cho có dạng \(at + b = 0\) với \(a\) và \(b\) là các hệ số đã cho nhưng \(a = 0\).
d) Phương trình \({x^2} + 3 = 0\) không là phương trình bậc nhất một ẩn vì không có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số (do có \({x^2}\)).

1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực

1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực

a: Phương trình có dạng ax+b=0 khi a<>0 được gọi là phương trình bậc nhất một ẩn
Phương trình 2x-5=2x+3 là phương trình bậc nhất một ẩn
c: Hai phương trình tương đương là hai phương trình có cùng tập nghiệm

a) Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.
b) Hệ đã cho có vô số nghiệm.

Em là học sinh lớp 7 nên em giải theo cách hiểu của em nhé:
a)* Định nghĩa
Phương trình ax + b = 0, với a và b là hai số đã cho và a # 0 được gọi là phương trình bậc nhất một ẩn
* Cách giải:
Bước 1: Chuyển vế ax = -b
Bước 2: Chia hai vế cho a: x = \(\frac{-b}{a}\)
Bước 3: Kết luận nghiệm: S = \(\frac{-b}{a}\)
Ta có thể trình bày ngắn gọn như sau:
ax + b = 0 <=> ax = -b <=> x = \(\frac{-b}{a}\)
Vậy tập nghiệm của phương trình là S = \(\left\{\frac{-b}{a}\right\}\)
b) Nếu giải theo mô hình trên, ta có:
\(A=2x+4=0\\ \Leftrightarrow2x=-4\\ \Leftrightarrow x=\frac{-4}{2}\\ \Leftrightarrow x=-2\)
Vậy tập nghiệm của phường trình A là: {-2}
Chúc chị học tốt!![]()


- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.
- Bạn Phương nhận xét sai.
Ví dụ: Xét hai hệ 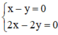 và
và 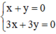
Hệ 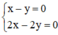 có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
Hệ 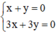 có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.
a) Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0 (với a ≠ 0)
Ví dụ: 2x + 4 = 0
a = 2; b = 4
b) Công thức tính thể tích hình hộp chữ nhật:
V = Sh
Với V là thể tích, S là diện tích 1 đáy, h là chiều cao
c)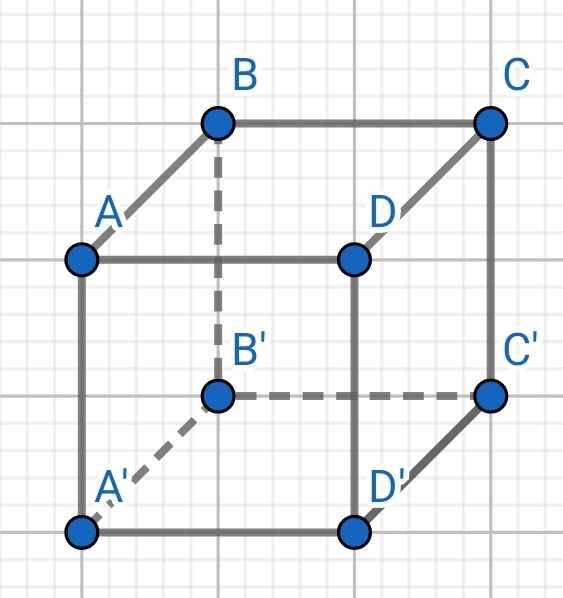
Thể tích:
V = AB.AD.AA'
= 12 . 16 . 25 = 4800 (cm³)
a: ax+b=0(a<>0) là phương trình bậc nhất một ẩn
b: V=a*b*c
a,b là chiều dài, chiều rộng
c là chiều cao
c: V=12*16*25=4800cm3