Vật sáng AB có dạng mũi tên đặt vuông góc với trục chính của thấu kính phân kỳ, A nằm trên trục chính và cách thấu kính một khoảng 36 cm, thấu kính có tiêu cự 12 cm. Biết vật AB có chiều cao 6 cm. a) Dựng ảnh A'B' của vật AB (Không cần đúng tỉ lệ) b) Vận dụng kiến thức hình học, hãy tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 4 2022
a, Ảnh ảo nhỏ hơn vật
b, Có CF//BC
\(\Rightarrow\dfrac{FO}{BK}=\dfrac{OB'}{BB'}=\dfrac{8}{12}=\dfrac{2}{3}\\ \Rightarrow\dfrac{OB'}{OB}=\dfrac{2}{3}\\ do.A'B'//AB\\ \Rightarrow\dfrac{AB'}{AB}=\dfrac{OB}{OB}=\dfrac{3}{4}=\dfrac{OA'}{OA}\\ \Rightarrow A'B'=...;OA'=....\)
TM
18 tháng 4 2023
a) Bạn tự vẽ hình.
b) Hình minh họa :
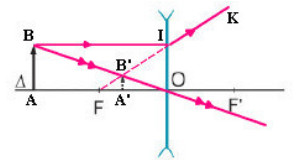
Xét \(\Delta FA'B'\sim\Delta FOI\) có : \(\dfrac{A'B'}{OI}=\dfrac{A'F}{OF}\Leftrightarrow\dfrac{A'B'}{AB}=\dfrac{OF-OA'}{OF}\)
\(\Rightarrow\dfrac{h'}{3}=\dfrac{15-d'}{15}\left(1\right)\)
Xét \(\Delta OA'B'\sim\Delta OAB\) có : \(\dfrac{A'B'}{AB}=\dfrac{OB'}{OB}\Leftrightarrow\dfrac{h'}{3}=\dfrac{d'}{30}\left(2\right)\).
Từ (1) và (2), ta có hệ phương trình : \(\left\{{}\begin{matrix}\dfrac{h'}{3}=\dfrac{15-d'}{15}\\\dfrac{h'}{3}=\dfrac{d'}{30}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d'=10\left(cm\right)\\h'=1\left(cm\right)\end{matrix}\right.\).
Vậy : Ảnh A'B' cách thấu kính \(d'=10\left(cm\right)\) và cao \(h'=1\left(cm\right)\).
H9
HT.Phong (9A5)
CTVHS
6 tháng 5 2023
Ta có:
\(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}=\dfrac{15}{OA'}\left(1\right)\)
\(\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}=\dfrac{OF'}{OA'-OF'}=\dfrac{30}{OA'-30}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{15}{OA'}=\dfrac{30}{OA'-30}\)
\(\Leftrightarrow15\left(OA'-30\right)=30OA'\)
\(\Leftrightarrow15OA'-450=30OA'\)
\(\Leftrightarrow-450=30OA'-15OA'\)
\(\Leftrightarrow-450=15OA'\)
\(\Leftrightarrow OA'=\dfrac{-450}{15}=-30\left(cm\right)\)
Vậy khoảng cách từ ảnh đến thấu kính là: -30cm
21 tháng 4 2023
a. Để vẽ ảnh của vật AB cho bởi thấu kính, ta sử dụng quy tắc chính của thấu kính phân kì:
Với vật đặt trước thấu kính, ta vẽ một tia đi qua đỉnh A của vật và tiếp tục đi thẳng qua thấu kính.Với vật đặt sau thấu kính, ta vẽ một tia đi từ đỉnh B của vật và tiếp tục đi thẳng qua thấu kính.b. Để xác định ảnh là ảnh thật hay ảnh ảo, ta sử dụng quy tắc sau:
Nếu ảnh xuất hiện ở cùng phía với vật (tức là nằm về phía mà tia đi từ vật đến thấu kính), thì ảnh là ảnh thật.Nếu ảnh xuất hiện ở phía ngược lại so với vật (tức là nằm về phía mà tia đi từ thấu kính đến mắt), thì ảnh là ảnh ảo.Trong trường hợp này, ta thấy ảnh xuất hiện ở cùng phía với vật, nên ảnh là ảnh thật.
c. Để tính khoảng cách giữa ảnh và thấu kính, ta sử dụng công thức:
1/f = 1/do + 1/di
Trong đó:
f là tiêu cự của thấu kínhdo là khoảng cách từ vật đến thấu kínhdi là khoảng cách từ ảnh đến thấu kínhThay các giá trị vào công thức, ta có:
1/20 = 1/30 + 1/di
=> di = 60 cm
Vậy, ảnh cách thấu kính 60 cm.
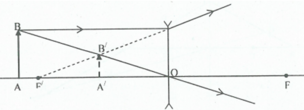
Ta có: \(\Delta ABO\sim\Delta A'B'O\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\left(1\right)\)
Và \(\Delta OIF\sim\Delta A'B'F\Rightarrow\dfrac{OF}{A'F}=\dfrac{OI}{A'B'}\left(2\right)\)
\(\Rightarrow\dfrac{OF}{OF-OA'}=\dfrac{OA}{OA'}\Rightarrow\dfrac{12}{12-OA'}=\dfrac{6}{OA'}\Rightarrow OA'=4\left(cm\right)\)
Ta có: \(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\Rightarrow A'B'=\dfrac{AB.OA}{OA'}=\dfrac{36.6}{4}=54\left(cm\right)\)
Vật ảnh cao 4cm và cách thấu kính 54cm