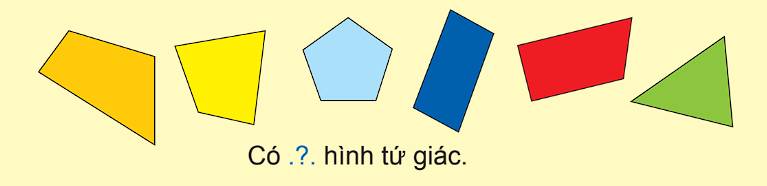
Hình nào không phải là hình tứ giác?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
1
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
a) Xét tứ giác \(ABCD\) ta có:
\(AB = CD\) (gt)
\(AD = BC\) (gt)
Suy ra: \(ABCD\) là hình bình hành
b) Xét tứ giác \(EFGH\) ta có:
\(\widehat {\rm{E}} = \widehat G\) (gt)
\(\widehat F = \widehat H\) (gt)
Suy ra \(EFGH\) là hình bình hành
c) Ta có: \(\widehat J = \widehat {\rm{K}} = 60^\circ \) (gt)
Mà hai góc ở vị trí so le trong
Suy ra \(IJ\) // \(KL\) (1)
Ta có: \(\widehat K + \widehat L = 60^\circ + 120^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(JK\;{\rm{//}}\;IL\) (2)
Từ (1), (2) suy ra \(IJKL\) là hình bình hành
d) Xét tứ giác \(MNPQ\) ta có:
\(O\) là trung điểm của \(NQ\) (do \(OQ = ON\))
\(O\) là trung điểm của \(MP\) (do \(OP = OM\))
Suy ra \(MNPQ\) là hình bình hành
e) Tứ giác \(TSRU\) không là hình bình hành
g) Ta có: \(\widehat {\rm{V}} + \widehat {\rm{X}} = 75^\circ + 105^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra: \(VZ\) // \(XY\)
Xét tứ giác \(VZYX\) ta có:
\(VZ\) // \(XY\) (cmt)
\(VZ = XY\) (gt)
Suy ra \(VZYX\) là hình bình hành
CM
7 tháng 12 2018
Đặt ê ke như hình vẽ để kiểm tra xem mỗi tứ giác có hay không hai cạnh song song.
+ Tứ giác ABCD có AB // CD nên là hình thang.
+ Tứ giác EFGH không có hai cạnh nào song song nên không phải hình thang.
+ Tứ giác KMNI có KM // IN nên là hình thang.
3 tháng 11 2018
bạn vẽ hình rồi lấy compa quay xem có trong hình tròn k là đc
PT
1
Hình màu tím, màu vàng, màu cam, màu đỏ