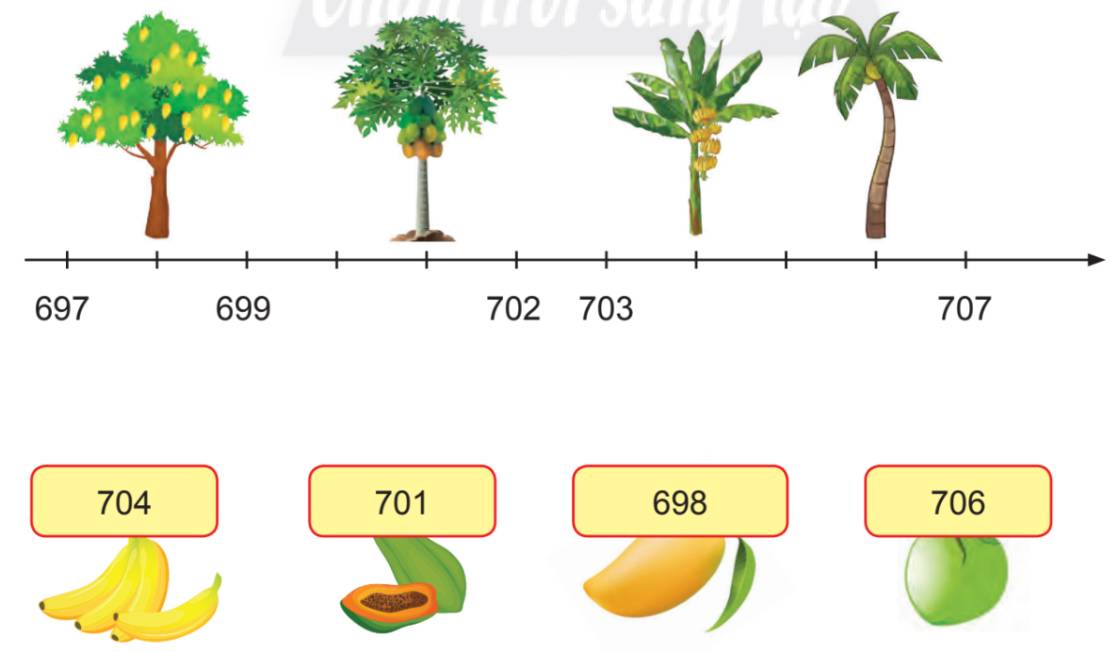
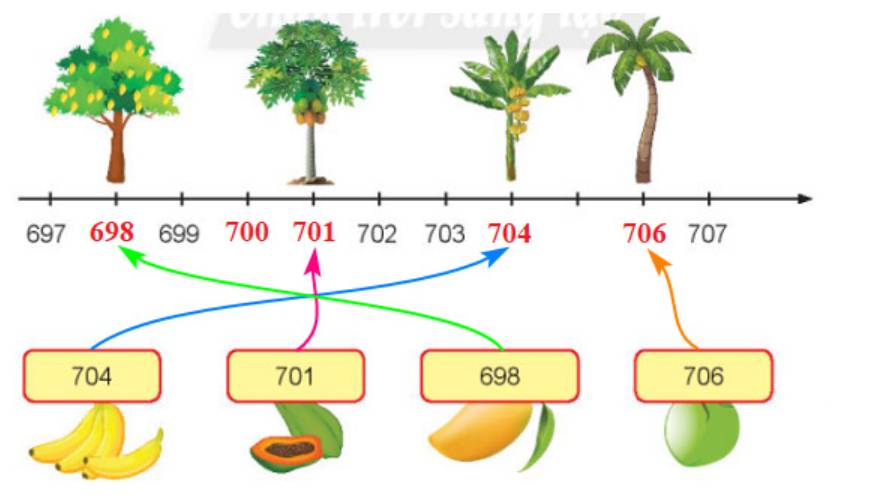
Chọn thẻ số thích hợp cho mỗi cây.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
QT
Quoc Tran Anh Le
Giáo viên
11 tháng 12 2023
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 11 2023
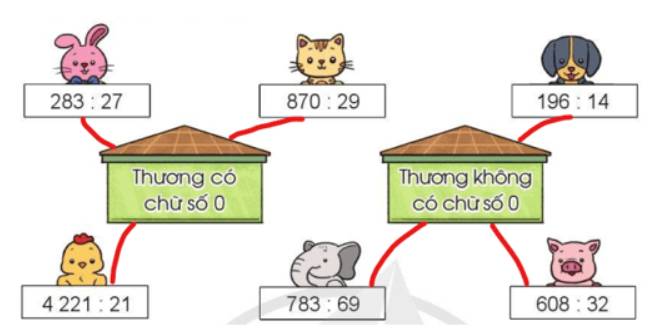
Ta có:
283 : 27 = 10 (dư 13)
870 : 29 = 30
196 : 14 = 14
4 221 : 21 = 201
783 : 69 = 11 (dư 24)
608 : 32 = 19
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
24 tháng 7 2023
Mèo: 2 kg
Voi: 5 tấn
Chó: 1 yến
Hươu cao cổ: 9 tạ
NT
1
HQ
Hà Quang Minh
Giáo viên
29 tháng 11 2023
Ví dụ:
Chọn 2 thẻ số 9 và 5, ta có phép nhân 9 x 5 = 45
Chọn hai thẻ số 5 và 4, ta có phép nhân 5 x 4 = 20
Làm tương tự với các thẻ số còn lại.
CM
12 tháng 10 2018
Chọn đáp án A.
Số phần tử của không gian mẫu là 
Tích ba số không chia hết cho 3 khi và chỉ khi cả ba số đó đều không chia hết cho 3. Các thẻ được viết số không chia hết cho 3 bao gồm 7 thẻ mang số 1; 2; 4; 5; 7; 8; 10. Số cách lấy được 3 thẻ mà tích ba số viết trên ba thẻ không chia hết cho 3 là C 7 3 = 35
Suy ra, số cách lấy được 3 thẻ mà tích ba số viết trên ba thẻ chia hết cho 3 là 
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Biến cố A là biến cố ngẫu nhiên vì các số ghi trên các tấm thẻ có cả số chẵn và số lẻ
Biến cố B là biến cố chắc chắn vì tất cả các tấm thẻ đều ghi số chia hết cho 3
Biến cố C là biến cố không thể vì các số ghi trên các tấm thẻ không có số nào chia hết cho 10.
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 2 của 20 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^2\) ( phần tử)
b) Gọi A là biến cố “Tích các số trên hai thẻ là số lẻ”
Để tích các số trên thẻ là số lẻ thì cả hai thẻ bốc được đểu phải là số lẻ vậy nên ta phải chọn ngẫu nhiên 2 thẻ từ 10 thẻ số lẻ. Do đó, số phần tử các kết quả thuận lợi cho biến cố A là tổ hợp chập 2 của 10 phần tử: \(n\left( A \right) = C_{10}^2\) ( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^2}}{{C_{20}^2}} = \frac{9}{{38}}\)