Tìm nghiệm đa thức M=0x^3 + 0x^2 + 2x +10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
0
CM
25 tháng 4 2018
Ta có 2 x - 1 > 0 x - m < 3 ⇔ x > 1 2 x ≤ 3 + m .
Hệ vô nghiệm khi và chỉ khi: m + 3 ≤ 1 2 ⇔ x ≤ - 5 2 .
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2021
Đáp án D là đáp án đúng
Thế tọa độ O lần lượt vào các đáp án thì A: \(2\le0\) (sai), B: \(2\le0\) (sai), C:\(-2\ge0\) (sai)
D: \(2\ge0\) (đúng)
31 tháng 7 2023
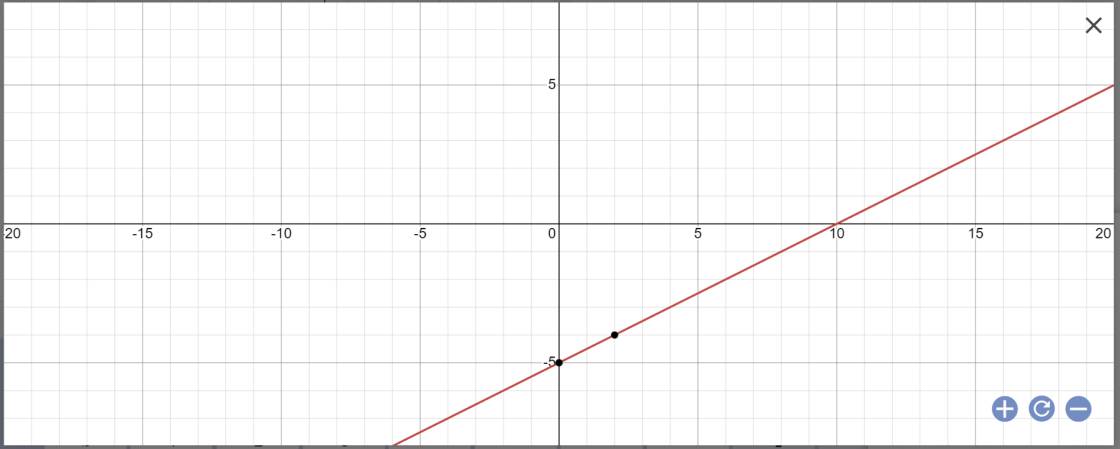
a: x-2y=5
=>2y=x-5
=>y=1/2x-5
Nghiệm tổng quát là: \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{1}{2}x-5\end{matrix}\right.\)
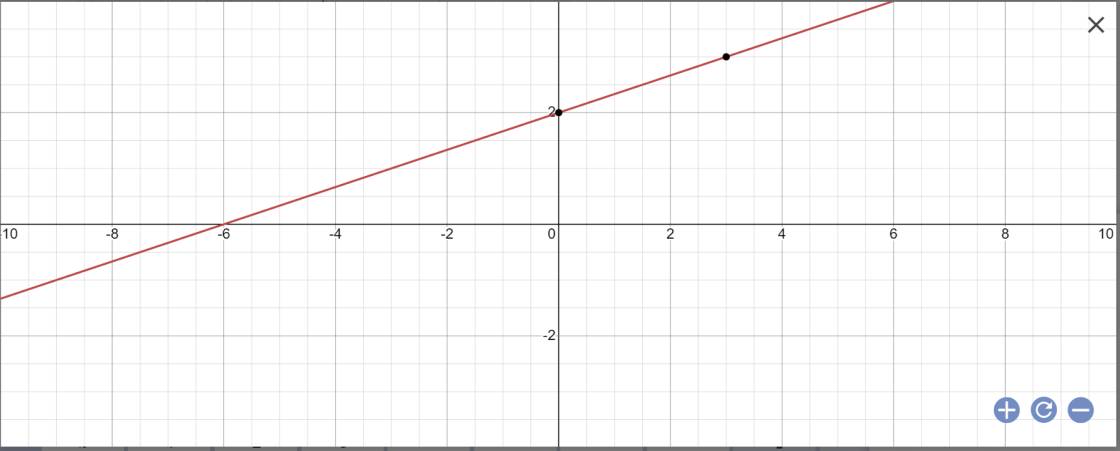
b: 3y-x=2
=>3y=x+2
=>y=1/3x+2
Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{1}{3}x+2\end{matrix}\right.\)
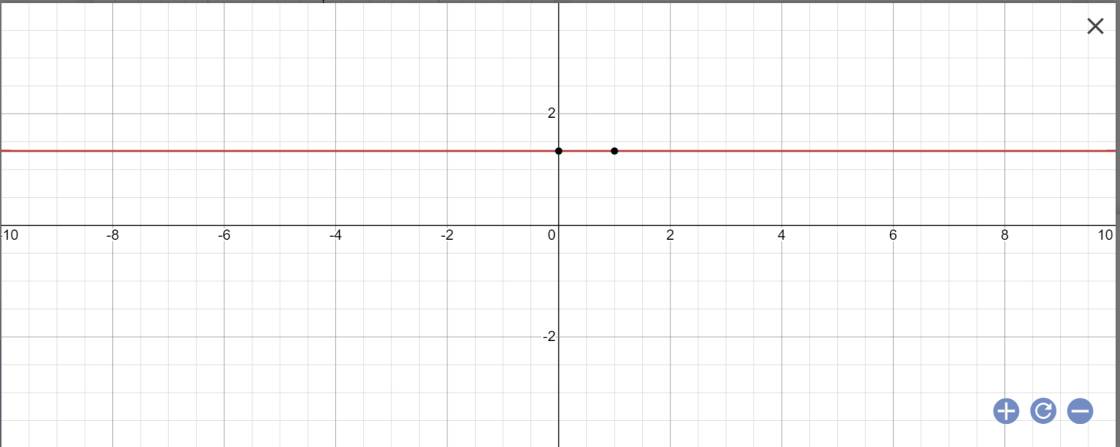
c: 0x+3y=4
=>3y=4
=>y=4/3
=>Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{4}{3}\end{matrix}\right.\)
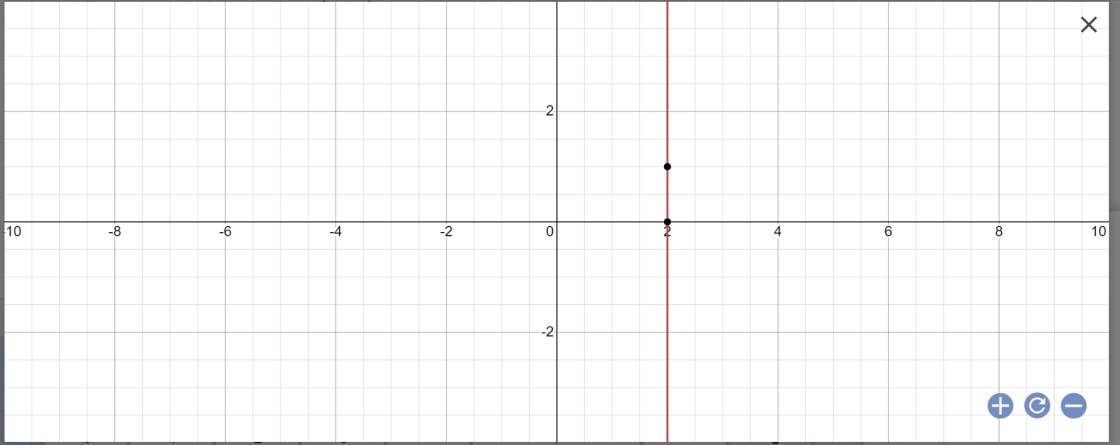
d: 2x+0y=4
=>2x=4
=>x=2
=>Nghiệm tổng quát là \(\left\{{}\begin{matrix}x=2\\y\in R\end{matrix}\right.\)
9 tháng 1
a: 2x-3y=5
=>3y=2x-5
=>\(y=\dfrac{2}{3}x-\dfrac{5}{3}\)
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{2}{3}x-\dfrac{5}{3}\end{matrix}\right.\)
Biểu diễn tập nghiệm:
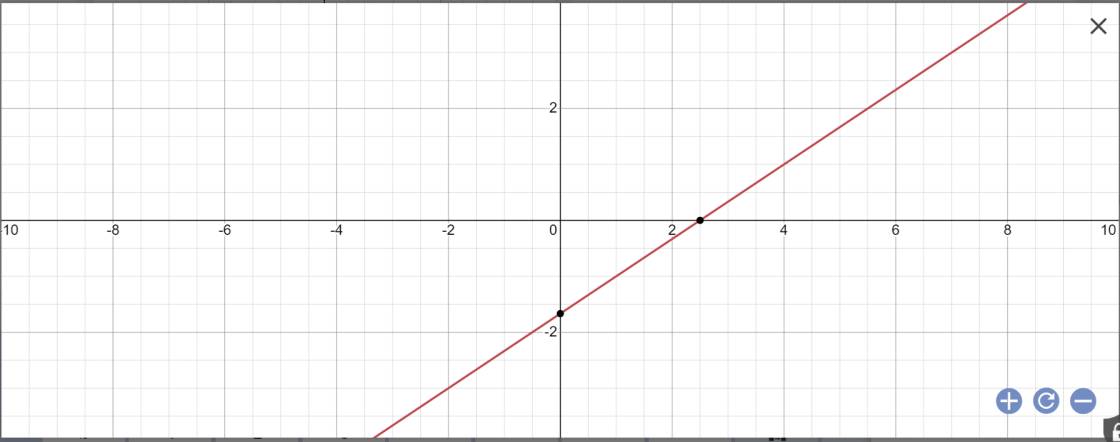
b: 4x+0y=12
=>4x=12
=>x=3
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x=3\\y\in R\end{matrix}\right.\)
Biểu diễn tập nghiệm:
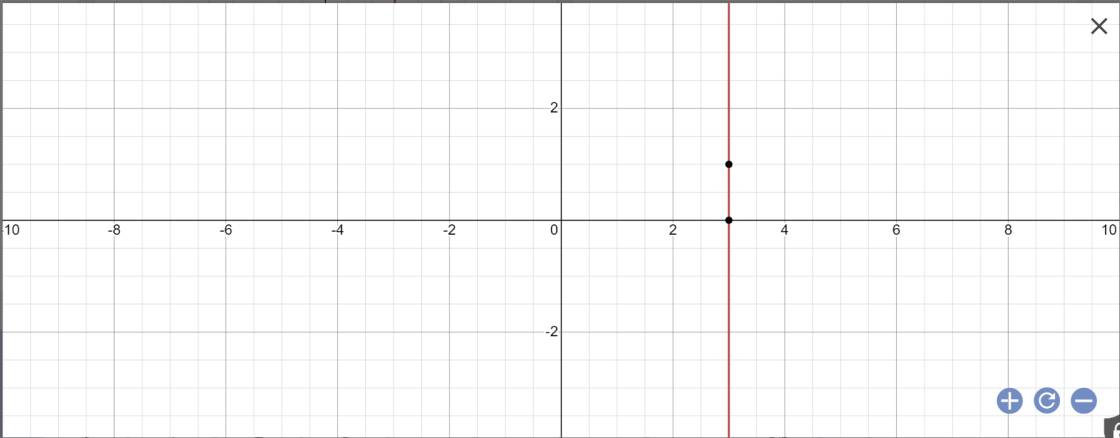
c: 0x-3y=6
=>-3y=6
=>y=-2
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=-2\end{matrix}\right.\)
Biểu diễn tập nghiệm:
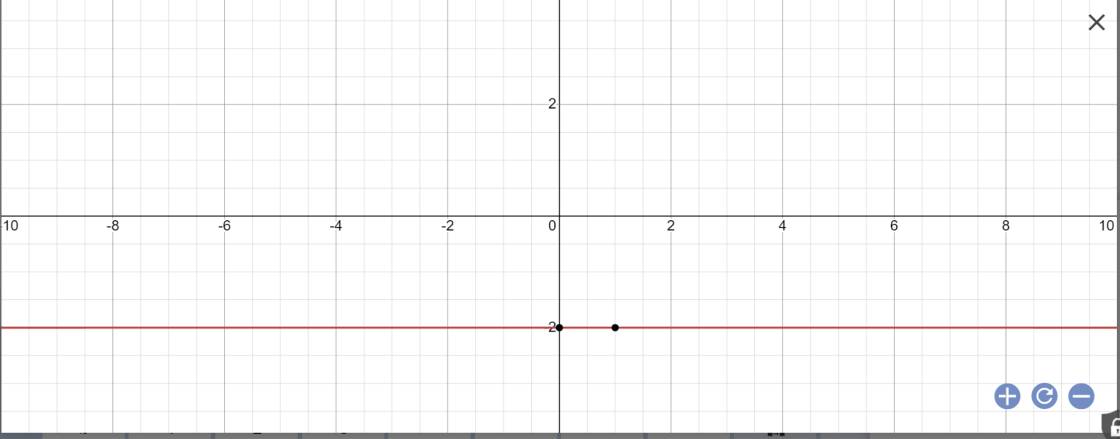
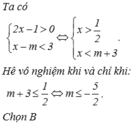
=> M = 2x + 10 = 0
<=> 2x = -10
<=> x = - 5
_Kik nha!! ^ ^
Suy ra 2x + 10 = 0
2x = -10
x = -10 : 2 = -5