Cho một con lắc đơn gồm có sợi dây dài 80cm và vật nặng có khối lượng 200g. Khi vật đang ở vị trí cân bằng thì truyền cho vật một vận tốc là \(2\sqrt{2}\) (m/s). Lấy g = 10m/s^2. Xác định vận tốc để vật có \(W_đ=3W_t\) lực căng của dây khi đó?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
26 tháng 4 2017
a. Chọn mốc thế năng tại vị trí cân bằng
W H = W A ⇒ 1 2 m v H 2 = m g z A ⇒ z A = v H 2 2 g = ( 2 2 ) 2 2.10 = 0 , 4 ( m )
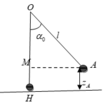
Mà z A = l − l cos α 0 ⇒ 0 , 4 = 0 , 8 − 0 , 8. cos α 0 ⇒ cos α 0 = 1 2 ⇒ α 0 = 60 0
Vậy vật có độ cao z= 0,4 m so với vị trí cân bằng và dây hợp với phương thẳng đứng một góc 60 0
b. Theo điều kiện cân bằng năng lượng
W A = W B m g z A = m g z B + 1 2 m v B 2 ⇒ 10.0 , 4 = 10.0 , 8 ( 1 − c o s 30 0 ) = 1 2 v B 2 ⇒ v B = 2 , 42 ( m / s )
Xét tại B theo định luật II Newton
P → + T → = m a →
Chiếu theo phương của dây
− P cos α + T = m v B 2 l ⇒ − 0 , 2.10. cos 30 0 + T = 0 , 2. 2 , 42 2 0 , 8 ⇒ T = 3 , 2 ( N )
c. Gọi C là vị trí để vật có vận tốc 2 ( m / s ) .
Theo định luật bảo toàn cơ năng
W A = W C ⇒ m g z A = 1 2 m v C 2 + m g z B ⇒ g z A = 1 2 v C 2 + g z C ⇒ 10.0 , 4 = 1 2 . ( 2 ) 2 + 10. z C ⇒ z C = 0 , 3 ( m )
Mà z C = l − l cos α C ⇒ cos α C = 5 8 ⇒ α C = 51 , 32 0
Xét tại C theo định luật II Newton P → + T → = m a →
Chiếu theo phương của dây
− P cos α C + T C = m v C 2 l ⇒ − 0 , 2.10. 5 8 + T C = 0 , 2. ( 2 ) 2 0 , 8 ⇒ T = 1 , 75 ( N )
d. Gọi D là vị trí để W d = 3 W t . Theo định luật bảo toàn cơ năng
W A = W D ⇒ m g z A = W dD + W t D ⇒ m g z A = 4 3 W dD ⇒ g z A = 4 3 . 1 2 v D 2 ⇒ 10.0 , 4 = 4 6 . v D 2 ⇒ v D = 6 ( m / s )
Mà v D = 2 g l ( cos α D − cos 60 0 ) ⇒ 6 = 2.10.0 , 8 ( cos α D − 0 , 5 ) ⇒ cos α D = 7 8
Xét tại D theo định luật II Newton P → + T → = m a →
Chiếu theo phương của dây
− P cos α D + T D = m v D 2 l ⇒ − 0 , 2.10. 7 8 + T D = 0 , 2. ( 6 ) 2 0 , 8 ⇒ T = 3 , 25 ( N )
VT
16 tháng 5 2019
Đáp án C
Gọi C là vị trí để vật có vận tốc 2 2 m / s
Theo định luật bảo toàn cơ năng
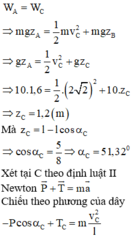
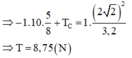
Chọn mốc thế năng tại vị trí cân bằng: \(W_H=W_A\Rightarrow\dfrac{1}{2}mv_H^2=mgh_A\)
\(\Rightarrow h_A=\dfrac{v_H^2}{2g}=\dfrac{\left(2\sqrt{2}\right)^2}{2.10}=0,4\left(m\right)\)
Mà \(h_A=l-lcos\left(\alpha_0\right)\)
\(\Rightarrow0,4=0,8-0,8.cos\left(\alpha_0\right)\)
\(\Rightarrow cos\left(\alpha_0\right)=\dfrac{1}{2}\Rightarrow\alpha_0=60^o\)
Gọi điểm B là vị trí để \(W_đ=3W_t\)
Theo định luật bảo toàn cơ năng:
\(W_A=W_B\)
\(\Leftrightarrow mgh_A=W_{đB}+W_{tB}\)
\(\Leftrightarrow mgh_A=\dfrac{4}{3}W_{đB}\)
\(\Leftrightarrow gh_A=\dfrac{4}{3}.\dfrac{1}{2}v_B^2\)
\(\Leftrightarrow10.0,4=\dfrac{4}{6}.v_B^2\)
\(\Leftrightarrow v_B=\sqrt{6}\left(m/s\right)\)
Mà \(v_B=\sqrt{2gl\left(cos\left(\alpha_B\right)-cos\left(60^o\right)\right)}\)
\(\Rightarrow\sqrt{6}=\sqrt{2.10.0,8.\left(cos\left(\alpha_B\right)-0,5\right)}\)
\(\Rightarrow cos\left(\alpha_B\right)=\dfrac{7}{8}\)
Xét tại B theo định luật II Newton :
\(\overrightarrow{P}+\overrightarrow{T}=m.\overrightarrow{a}\)
Chiếu theo phương của dây
\(-Pcos\left(\alpha_B\right)+T_B=m\dfrac{v_B^2}{l}\)
\(\Rightarrow-0,2.10\dfrac{7}{8}+T_B=0,2.\dfrac{\left(\sqrt{6}\right)^2}{0,8}\)
\(\Rightarrow T=3,25N\)