Đội múa có 1 bạn nam và 5 bạn nữ, Chọn ngẫu nhiên 1 bạn để phỏng vấn (biết khả năng được chọn của mỗi bạn là như nhau). Hãy tính xác suất của biến cố bạn được chọn là nam.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
2 tháng 5 2023
Chọn 1 bạn nam có 1 cách.
Chọn 1 bạn trong 5 bạn nữ có \(C_5^1=5\) cách
Theo quy tắc cộng, ta có : \(1+5=6\) cách chọn 1 bạn để phỏng vấn.
\(\Rightarrow n\left(\Omega\right)=6\)
Gọi \(A:``\) Bạn được chọn ngẫu nhiên là nam \("\)
Do trong đội múa chỉ có 1 nam nên \(\Rightarrow n\left(A\right)=1\)
Xác suất của biến cố A là \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{1}{6}\)
2 tháng 5 2023
Chị ơi, xác suất của lớp \(7\) không dùng được cách giải này ạ!
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Vì trong 5 bạn có 1 bạn trai nên xác suất của biến cố bạn được chọn là nam là \(\dfrac{1}{{1 + 5}} = \dfrac{1}{6}\)
AH
Akai Haruma
Giáo viên
4 tháng 5 2023
Lời giải:
Chọn 1 bạn từ trong 6 bạn, có 6 cách chọn
Chọn ngẫu nhiên 1 bạn mà bạn đó là nam, có duy nhất 1 cách chọn (do trong đội chỉ có 1 nam)
Xác suất để bạn được chọn là nam là: $1:6=\frac{1}{6}$
11 tháng 5 2023
Chọn 1 bạn nam có 1 cách.
Chọn 1 bạn trong 5 bạn nữ có cách
Theo quy tắc cộng, ta có : cách chọn 1 bạn để phỏng vấn.
Gọi Bạn được chọn ngẫu nhiên là nam
Do trong đội múa chỉ có 1 nam nên
Xác suất của biến cố A là
NB
Nguyễn Bích Ngọc
VIP
22 tháng 2
Tổng số học sinh là HS
Xác suất của biến cố bạn được chọn là nam là \(\dfrac{1}{6}\)
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_{45}^2.C_{45}^2\)
a) Gọi A là biến cố “Trong 4 bạn được chọn có ít nhất 1 bạn nam”, ta có biến cố đối \(\overline A \): “Trong 4 bạn được chọn không có bạn nam nào”
\(\overline A \) xảy ra khi các bạn được chọn đều là nữ. Số kết quả thuận lợi cho biến cố \(\overline A \) là \(n\left( {\overline A } \right) = C_{20}^2.C_{24}^2\)
Xác suất của biến cố \(\overline A \) là \(P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = \frac{{C_{20}^2.C_{24}^2}}{{C_{45}^2.C_{45}^2}} = \frac{{874}}{{16335}}\)
Suy ra, xác suất của biến cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{874}}{{16335}} = \frac{{15461}}{{16335}}\)
b) Gọi A là biến cố “Trong 4 bạn được chọn có đủ cả nam và nữ” ta có biến cố đối \(\overline A \): “Trong 4 bạn được chọn đều là nữ hoặc đều là nam”
\(\overline A \) xảy ra khi các bạn được chọn đều là nữ hoặc nam. Số kết quả thuận lợi cho biến cố \(\overline A \) là \(n\left( {\overline A } \right) = C_{20}^2.C_{24}^2 + C_{25}^2.C_{21}^2\)
Xác suất của biến cố \(\overline A \) là \(P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = \frac{{C_{20}^2.C_{24}^2 + C_{25}^2.C_{21}^2}}{{C_{45}^2.C_{45}^2}} = \frac{{1924}}{{16335}}\)
Suy ra, xác suất của biến cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{1924}}{{16335}} = \frac{{14411}}{{16335}}\)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) Hai biến cố A và B đồng khả năng vì đều có 5 khả năng cô gọi trúng bạn nam và 5 khả năng cô gọi trúng bạn nữ
b) Vì có 2 biến cố đồng khả năng và luôn xảy ra 1 trong 2 biến cố A và B nên xác suất của mỗi biến cố đó là \(\dfrac{1}{2}\)
CM
13 tháng 8 2018
Chọn B.
Không gian mẫu có số phần tử là 
.
Gọi A là biến cố: “Trong 5 bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ”. Khi đó, số kết quả thuận lợi cho biến cố A là: 
.
Vậy xác suất cần tính là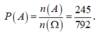 
.
Tổng số cách chọn ra một bạn để phỏng vấn là: 1+5 = 6
Xác suất biến cố bạn nam được chọn là:
\(\left(1:6\right)=\dfrac{1}{6}\approx16,66\%\)
Đs...
Tổng số cách chọn ra một bạn để phỏng vấn là: 1+5 = 6
Xác suất biến cố bạn nam được chọn là:
(1:6)=16≈16,66%(1:6)=61≈16,66%