Chứng minh a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 5 2021
a )
`VP= (a+b)^3-3ab(a+b)`
`=a^3+3a^2b+3ab^2+b^3-3a^2b-3ab^2`
`=a^3+b^3 =VT (đpcm)`
b)
b) Ta có
`VT=a3+b3+c3−3abc`
`=(a+b)3−3ab(a+b)+c3−3abc`
`=[(a+b)3+c3]−3ab(a+b+c)`
`=(a+b+c)[(a+b)2+c2−c(a+b)]−3ab(a+b+c)`
`=(a+b+c)(a2+b2+2ab+c2−ac−bc−3ab)`
`=(a+b+c)(a2+b2+c2−ab−bc−ca)=VP`
14 tháng 5 2021
a) Ta có:
`VP= (a+b)^3-3ab(a+b)`
`=a^3 + b^3+3ab ( a + b )- 3ab ( a + b )`
`=a^3 + b^3=VT(dpcm)`
b) Ta có
`VT=a^3+b^3+c^3−3abc`
`=(a+b)^3−3ab(a+b)+c^3−3abc`
`=[(a+b)^3+c^3]−3ab(a+b+c)`
`=(a+b+c)[(a+b)^2+c^2−c(a+b)]−3ab(a+b+c)`
`=(a+b+c)(a^2+b^2+2ab+c^2−ac−bc−3ab)`
`=(a+b+c)(a^2+b^2+c^2−ab−bc−ca)=VP`
VN
1
3 tháng 7 2023
a^3+b^3+c^3-3abc
=(a+b)^3+c^3-3ab(a+b)-3bca
=(a+b+c)(a^2+2ab+b^2-ac-bc+c^2)-3ab(a+b+c)
=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)
NA
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
Đặt \(P=\dfrac{a^3}{a^2+b^2+ab}+\dfrac{b^3}{b^2+c^2+bc}+\dfrac{c^3}{c^2+a^2+ca}\)
Ta có: \(\dfrac{a^3}{a^2+b^2+ab}=a-\dfrac{ab\left(a+b\right)}{a^2+b^2+ab}\ge a-\dfrac{ab\left(a+b\right)}{3\sqrt[3]{a^3b^3}}=a-\dfrac{a+b}{3}=\dfrac{2a-b}{3}\)
Tương tự: \(\dfrac{b^3}{b^2+c^2+bc}\ge\dfrac{2b-c}{3}\) ; \(\dfrac{c^3}{c^2+a^2+ca}\ge\dfrac{2c-a}{3}\)
Cộng vế:
\(P\ge\dfrac{a+b+c}{3}=673\)
Dấu "=" xảy ra khi \(a=b=c=673\)
Y
22 tháng 8 2018
a) Áp dụng nhiều lần công thức \(\left(x+y\right)^3=x^3-y^3+3xy\left(x+y\right)\), ta có:
\(\left(a+b+c\right)^3-a^3-b^3-c^3\)
\(=\left[\left(a+b\right)+c\right]^3-a^3-b^3-c^3\)
\(=\left(a+b\right)^3+c^3+3c\left(a+b\right)\left(a+b+c\right)-a^3-b^3-c^3\)
\(=a^3+b^3+3ab\left(a+b\right)+c^3+3c\left(a+b\right)\left(a+b+c\right)-a^3-b^3-c^3\)
\(=3\left(a+b\right)\left(ab+ac+bc+c^2\right)\)
\(=3\left(a+b\right)\left[a\left(b+c\right)+c\left(b+c\right)\right]\)
\(=3\left(a+b\right)\left(b+c\right)\left(a+c\right)\left(Đpcm\right)\)
b) Ta có:
\(a^3+b^3+c^3-3abc\)
\(=a^3+3ab\left(a+b\right)+b^2+c^3-3abc-3ab\left(a+b\right)\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ac-bc-ab\right)\)
Mình nghĩ bằng thế này mới đúng, bạn chắc ghi sai đề rồi 
22 tháng 8 2018
a) Ta có: (a + b + c)3 - a3 - b3 - c3 = [ (a + b + c)3 - a3 ] - ( b3 + c3)
= (a + b + c - a) ( a2 + b2 + c2 + 2ab + 2bc + 2ac + a2 + ab + ac + a2) - (b + c) ( b2 - bc + c3)
= (b + c) ( 3a2 + b2 + c2 + 3ab + 2bc + 3ac) - (b + c) ( b2 - bc + c3)
= ( b + c) ( 3a2 + b2 + c2 + 3ab + 2bc + 3ac - b2 + bc - c3)
= ( b + c) ( 3a2 + 3ab + 3bc + 3ac)
= 3 (b + c) [a (a + b) + c (a + b)]
= 3 (b + c) (a + b) (a + c) (đpcm)
25 tháng 7 2021
d) Ta có: \(a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)\cdot c+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)\)
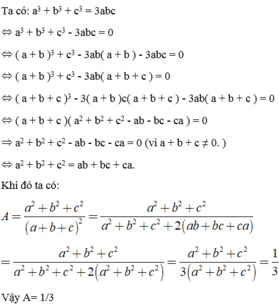
\(a^3+b^3+c^3-3abc=\left(a+b\right)^3+c^3-3a^2b-3ab^2-3abc=\left(a+b+c\right)^3\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+b^2+2ab-ac-bc+c^2\right)-3ab\left(a+b+c\right)=\left(a+b+c\right)\left(a^2+b^2+2ab-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)\)
Nhưng theo mình thấy a^3+b^3+c^3 không thể đổi thành (a+b+c)^3