Có hai túi đựng bi: túi số 1 có 3 bi đỏ, 2 bi xanh và túi số 2 có 4 bi đổ, 5 bi xanh. Từ mỗi túi lấy ngẫu nhiên ra 1 bi. Tính xác suất để lấy ra 2 bi cùng màu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì hai túi là khác nhau nên biến cố lấy một viên bi mỗi túi là độc lập.
Gọi biến cố A: “Hai viên bi được lấy có cùng màu xanh”, biến cố B: “Hai viên bi được lấy có cùng màu đỏ”, biến cố C: “Hai viên bi được lấy có cùng màu”
a) Xác suất lấy được viên bi màu xanh từ túi I là \(\frac{3}{{10}}\)
Xác suất lấy được viên bi màu xanh từ túi II là \(\frac{{10}}{{16}} = \frac{5}{8}\)
Xác suất lấy được hai viên bi cùng màu xanh là \(\frac{3}{{10}}.\frac{5}{8} = \frac{3}{{16}}\)
b) Xác suất lấy được viên bi màu đỏ từ túi I là \(\frac{7}{{10}}\)
Xác suất lấy được viên bi màu đỏ từ túi II là \(\frac{6}{{16}} = \frac{3}{8}\)
Xác suất lấy được hai viên bi cùng màu đỏ là \(\frac{7}{{10}}.\frac{3}{8} = \frac{{21}}{{80}}\)
c) Ta có \(C = A \cup B\) mà A và B xung khắc nên
\(P\left( C \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) = \frac{3}{{16}} + \frac{{21}}{{80}} = \frac{9}{{20}}\)
Vậy xác suất để hai viên bi được lấy có cùng màu là \(\frac{9}{{20}}.\)
d) Gọi biến cố D: “Hai viên bi được lấy không cùng màu”
Khi đó \(\overline D = C\)
\( \Rightarrow P\left( D \right) = 1 - P\left( {\overline D } \right) = 1 - P\left( C \right) = 1 - \frac{9}{{20}} = \frac{{11}}{{20}}\)
Vậy xác suất để hai viên bi được lấy không cùng màu là \(\frac{{11}}{{20}}.\)

a) Cách lấy 2 viên bi trong túi là:
Xanh – đỏ; Xanh – trắng; Xanh – vàng; Đỏ - trắng; Đỏ - vàng; Trắng – vàng.
Có 6 cách lấy hai biên bi từ trong túi.
Biến cố \(A\) xảy ra khi 2 viên bi lấy ra có 1 viên bi màu đỏ
Có 3 kết quả thuận lợi cho biến cố \(A\) là Xanh – đỏ; Đỏ - trắng; Đỏ - vàng
Xác suất 2 viên bi lấy ra có 1 viên bi màu đỏ là \(\frac{3}{6} = \frac{1}{2}\).
Vậy xác suất 2 viên bi lấy ra có 1 viên bi màu đỏ là \(\frac{1}{2}\).
b) Biến cố \(B\) xảy ra khi 2 viên bi lấy ra đều không có màu trắng
Có 3 kết quả thuận lợi cho \(B\) là : Xanh – đỏ; Xanh – vàng; Đỏ - vàng.
Xác suất 2 viên bi lấy ra không có viên bi nào màu trắng là \(\frac{3}{6} = \frac{1}{2}\).
Vậy xác suất 2 viên bi lấy ra không có viên bi nào màu trắng là \(\frac{1}{2}\).

a: n(omega)=4+3+3+5=15
n(xanh)=4+3=7
=>P=7/15
b: P=7/15*4/7=4/15

a) Để biến cố “ Người chơi thắng” là biến cố chắc chắn thì người chơi luôn phải lấy được viên bi màu đỏ. Mà túi 1 toàn là bi đen nên túi 2 cần toàn là bi đỏ thì người chơi luôn lấy được bi đỏ
b) Để biến cố “ Người chơi thắng” là biến cố không thể thì người chơi luôn không lấy được viên bi màu đỏ. Vì túi 1 toàn là bi đen nên túi 2 không được có bi đỏ
c) Để biến cố “ Người chơi thắng” là biến cố ngẫu nhiên thì người chơi có thể lấy được viên bi màu đỏ. Mà túi 1 toàn là bi đen nên túi 2 cần có chứa bi đỏ và thêm bi màu khác.
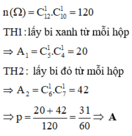

Lấy ngẫu nhiên từ mỗi túi 1 viên bi: \(C^1_5.C^1_9\) ( cách )
Trường hợp 1: Lấy ra từ mỗi túi 1 viên bi đỏ:
\(C^1_3.C^1_4\) ( cách )
Trường hợp 2: Lấy ra từ mỗi túi 1 viên bi xanh
\(C^1_2.C^1_5\) ( cách )
Xác suất lấy được 2 bi cùng màu là: \(\dfrac{C^1_3.C^1_4+C^1_2.C^1_5}{C^1_5.C^1_9}=\dfrac{22}{45}\)
Lấy ngẫu nhiên 1 bi từ các túi có :
\(TH1:\) Lấy 1 bi từ túi số 1 có 3 bi đỏ và 2 bi xanh có \(C^1_5\) cách
\(TH2:\) Lấy 1 bi từ túi số 2 có 4 bi đỏ, 5 bi xanh có \(C_9^1\) cách
Theo quy tắc cộng, ta có \(C_5^1+C_9^1=14\) cách lấy ngẫu nhiên 1 bi từ các túi.
Vậy \(n\left(\Omega\right)=14\)
Gọi \(A:``\) Lấy ra 2 bi cùng màu \("\)
\(TH1:\) Lấy ra mỗi túi 1 bi đỏ có \(C^1_3.C_4^1\) cách
\(TH2:\) Lấy ra mỗi túi 1 bi xanh có \(C_2^1.C_5^1\) cách
Theo quy tắc cộng, ta có \(C^1_3.C_4^1+C_2^1.C^1_5=22\)
\(\Rightarrow n\left(A\right)=22\)
Xác suất \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{22}{14}=\dfrac{11}{7}\)