giải phương trình (x-2)2(x-9) = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a,(x+3)(x^2+2021)=0`
`x^2+2021>=2021>0`
`=>x+3=0`
`=>x=-3`
`2,x(x-3)+3(x-3)=0`
`=>(x-3)(x+3)=0`
`=>x=+-3`
`b,x^2-9+(x+3)(3-2x)=0`
`=>(x-3)(x+3)+(x+3)(3-2x)=0`
`=>(x+3)(-x)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=-3\end{array} \right.$
`d,3x^2+3x=0`
`=>3x(x+1)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=-1\end{array} \right.$
`e,x^2-4x+4=4`
`=>x^2-4x=0`
`=>x(x-4)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=4\end{array} \right.$
1) a) \(\left(x+3\right).\left(x^2+2021\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^2+2021=0\end{matrix}\right.\\\left[{}\begin{matrix}x=-3\left(nhận\right)\\x^2=-2021\left(loại\right)\end{matrix}\right. \)
=> S={-3}

Bài 9:
Không, vì $x+2=0$ có nghiệm duy nhất $x=-2$ còn $\frac{x}{x+2}=0$ ngay từ đầu đkxđ đã là $x\neq -2$ (cả 2 pt không có cùng tập nghiệm)
Bài 8:
a. Khi $m=2$ thì pt trở thành:
$(2^2-9)x-3=2$
$\Leftrightarrow -5x-3=2$
$\Leftrightarrow -5x=5$
$\Leftrightarrow x=-1$
b.
Khi $m=3$ thì pt trở thành:
$(3^2-9)x-3=3$
$\Leftrightarrow 0x-3=3$
$\Leftrightarrow 0=6$ (vô lý)
c. Khi $m=3$ thì pt trở thành:
$[(-3)^2-9]x-3=-3$
$\Leftrightarrow 0x-3=-3$ (luôn đúng với mọi $x\in\mathbb{R}$)
Vậy pt vô số nghiệm thực.

a, ĐK: \(x\le-1,x\ge3\)
\(pt\Leftrightarrow2\left(x^2-2x-3\right)+\sqrt{x^2-2x-3}-3=0\)
\(\Leftrightarrow\left(2\sqrt{x^2-2x-3}+3\right).\left(\sqrt{x^2-2x-3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2-2x-3}=-\dfrac{3}{2}\left(l\right)\\\sqrt{x^2-2x-3}=1\end{matrix}\right.\)
\(\Leftrightarrow x^2-2x-3=1\)
\(\Leftrightarrow x^2-2x-4=0\)
\(\Leftrightarrow x=1\pm\sqrt{5}\left(tm\right)\)
b, ĐK: \(-2\le x\le2\)
Đặt \(\sqrt{2+x}-2\sqrt{2-x}=t\Rightarrow t^2=10-3x-4\sqrt{4-x^2}\)
Khi đó phương trình tương đương:
\(3t-t^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=0\\t=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2+x}-2\sqrt{2-x}=0\\\sqrt{2+x}-2\sqrt{2-x}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2+x=8-4x\\2+x=17-4x+12\sqrt{2-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\left(tm\right)\\5x-15=12\sqrt{2-x}\left(1\right)\end{matrix}\right.\)
Vì \(-2\le x\le2\Rightarrow5x-15< 0\Rightarrow\left(1\right)\) vô nghiệm
Vậy phương trình đã cho có nghiệm \(x=\dfrac{6}{5}\)

a: \(\Leftrightarrow\left(x-\sqrt{5}\right)^2=0\)
\(\Leftrightarrow x-\sqrt{5}=0\)
hay \(x=\sqrt{5}\)
b: \(\Leftrightarrow4x^4-9x^2+4x^2-9=0\)
\(\Leftrightarrow4x^2-9=0\)
=>x=3/2hoặc x=-3/2

a. \(x-\dfrac{x+2}{3}< 3x+\dfrac{x}{2}+5\)
\(\Leftrightarrow\dfrac{6x}{6}-\dfrac{2\left(x+2\right)}{6}< \dfrac{18x}{6}+\dfrac{3x}{6}+\dfrac{30}{6}\)
\(\Rightarrow6x-2x-4-18x-3x-30< 0\)
\(\Leftrightarrow-17x< 34\)
\(\Leftrightarrow x>-2\)
b. \(\dfrac{x}{2}+\dfrac{1-x}{3}>0\)
\(\Leftrightarrow3x+2-2x>0\)
\(\Leftrightarrow x>-2\)
c. \(\left(x-9\right)^2-x\left(x+9\right)< 0\)
\(\Leftrightarrow x^2-18x+81-x^2-9x< 0\)
\(\Leftrightarrow-27x< -81\)
\(\Leftrightarrow x>3\)

Bạn coi lại đề câu a, chỗ \(\log_5-x\) đó
b.
\(\Leftrightarrow9^x-3^x-2.3^x-2=0\)
\(\Leftrightarrow3^x\left(3^x-1\right)-2\left(3^x-1\right)=0\)
\(\Leftrightarrow\left(3^x-2\right)\left(3^x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3^x=2\\3^x=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\log_32\\x=0\end{matrix}\right.\)

\(\left(x+2\right)\left(9-3x\right)=0\)
\(3\left(x+2\right)\left(3-x\right)=0\)
\(\left(x+2\right)\left(3-x\right)=0\)
=> x+2 =0 hoặc 3-x=0
=> x=-2 hoặc x=3

\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)}{\left(3-x\right)\left(3+x\right)}>0\)
Bảng xét dấu:
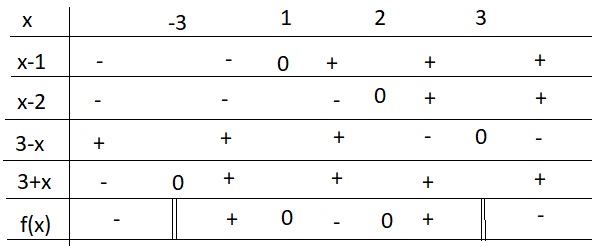
Từ bảng xét dấu ta có nghiệm của BPT là: \(x\in\left(-3;1\right)\cup\left(2;3\right)\)
\(\left(x-2\right)^2\left(x-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-2\right)^2=0\\x-9=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-2\right)\left(x-2\right)=0\\x=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=9\end{matrix}\right.\)
\(\left(x-2\right)^2\left(x-9\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-2\right)\left(x-9\right)=0\)
\(\Leftrightarrow x-2=0hoặcx-9=0\)
\(\Leftrightarrow x=2hoặcx=9\)
Vậy phương trình có nghiệm là:\(S=\left\{2;9\right\}\)