Cho hàm số y = (m + 1)sinx + mcosx - (m+2)x + 1. Tìm giá trị của m để y' = 0 có nghiệm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
y' = (m + 1)cosx – msinx – ( m + 2)
Phương trình y’ = 0 ⇔ (m + 1)cosx – msinx = (m + 2)
Điều kiện phương trình có nghiệm là a2 + b2 ≥ c2
⇔ (m + 1)2 + m2 ≥ (m + 2)2 ⇔ m2 – 2m – 3 ≥ 0 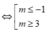

1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)

Chọn A
Điều kiện: ![]() . Điều kiện cần để hàm số
. Điều kiện cần để hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() là
là![]() .
.
Ta có : 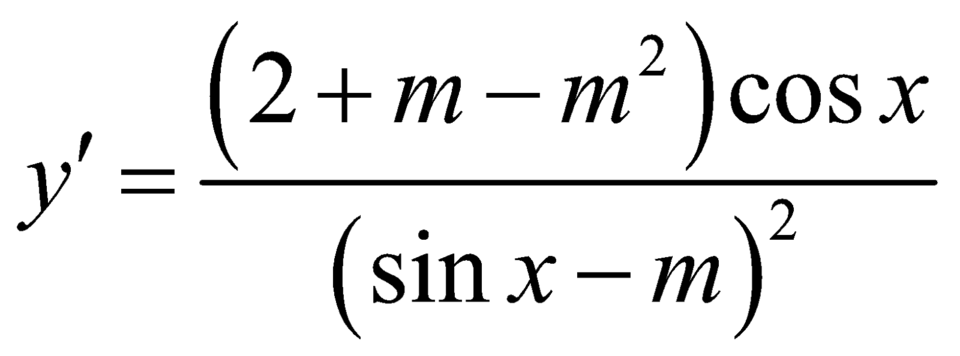 .
.
Ta thấy ![]()
![]() .
.
Để ham số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() là
là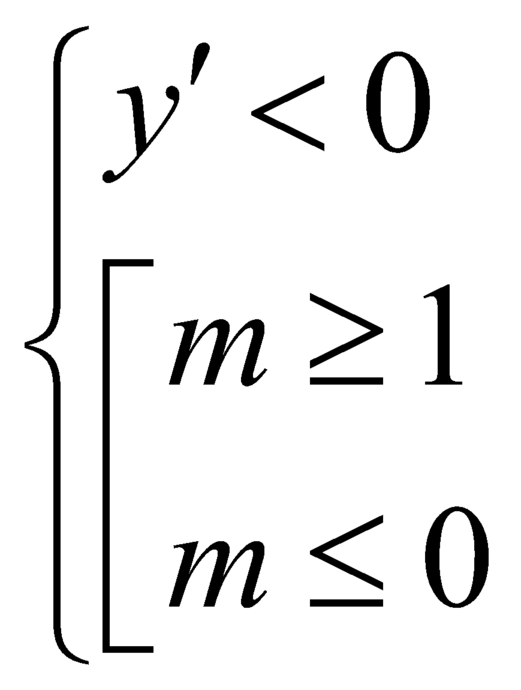
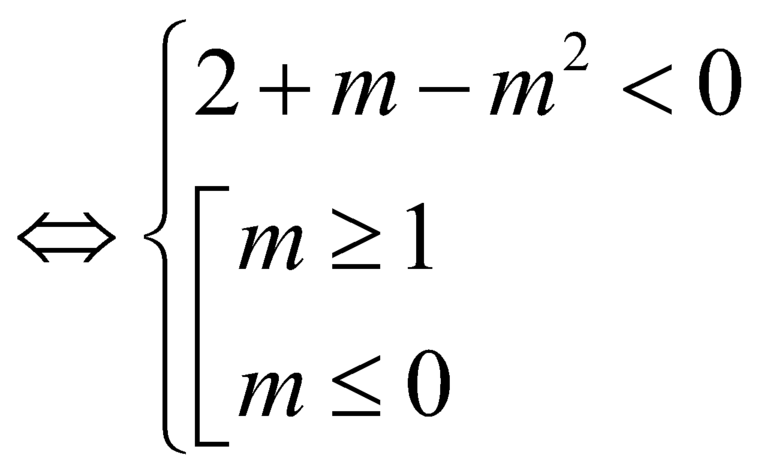
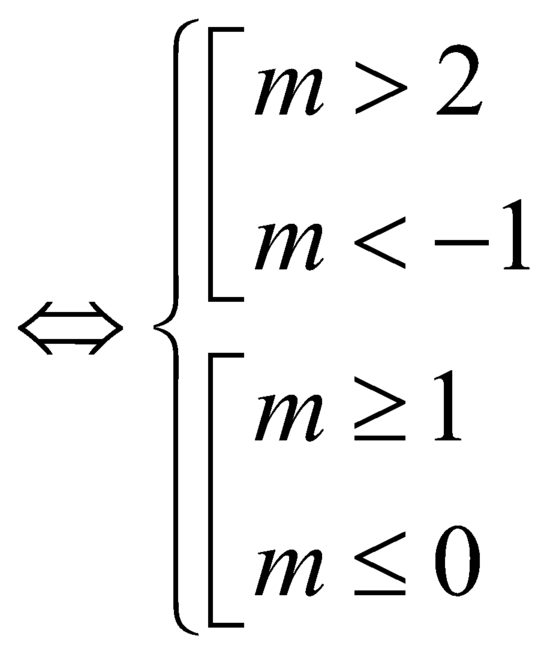
![]() .
.

Chọn D.
Cách 1:
![]()
![]()
Hàm số y = 2 cos 3 x - 3 cos 2 x - m cos x nghịch biến trên khoảng 0 ; π 2
![]()

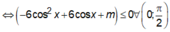
![]()
Xét 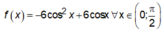
Đặt t = cosx
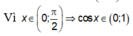
Ta có: ![]() là Parabol có đỉnh
là Parabol có đỉnh 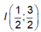 và hệ số a < 0 nên có giá trị lớn nhất là
3
2
tại t =
1
2
và hệ số a < 0 nên có giá trị lớn nhất là
3
2
tại t =
1
2
Để (1) xảy ra 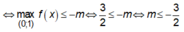
Cách 2:
Đặt t = cosx
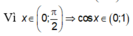
Ta có:
![]()
Hàm số y =
2
cos
3
x
-
3
cos
2
x
-
m
cos
x
nghịch biến trên khoảng
0
;
π
2
thì ![]() đồng biến trên khoảng (0;1)
đồng biến trên khoảng (0;1)
![]()
![]()
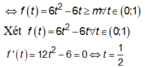
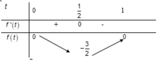
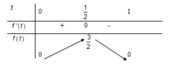
Dựa vào bảng biến thiên suy ra ![]()
\(y'=\left(m+1\right)cosx-msinx-\left(m+2\right)\)
\(y'=0\Rightarrow\left(m+1\right)cosx-msinx=m+2\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất, pt đã cho có nghiệm khi:
\(\left(m+1\right)^2+m^2\ge\left(m+2\right)^2\)
\(\Leftrightarrow m^2-2m-3\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-1\end{matrix}\right.\)