Một tổ có 8 học sinh nam và 7 học sinh nữ. Chia tổ thành 3 nhóm mỗi nhóm 5 người để làm 3 nhiệm vụ khác nhau. Tính xác suất để khi chia ngẫu nhiên nhóm nào cũng có nữ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 3 2018
Đáp án A
Không gian mẫu: C 12 4 . C 8 4 . 1 = 34650
Chỉ có 3 nữ và chia mỗi nhóm có đúng 1 nữ và 3 nam.
Nhóm 2 có C 3 1 . C 9 3 = 252 cách.
Lúc đó còn lại 2 nữ, 6 nam, nhóm thứ 2 có :
C 2 1 . C 9 3 = 40 cách chọn.
Cuối cùng còn 4 người là một nhóm: có 1 cách.
Theo quy tắc nhân thì có: 252.40.2=10080 cách.
Vậy xác suất cần tìm là: P = 10080 34650 = 16 55 .
CM
1 tháng 6 2019
Đáp án A
Không gian mẫu C 12 4 . C 8 4 . 1 = 34650 . Chỉ có 3 nữ và chia mỗi nhóm có đúng 1 nữ và 3 nam.
Nhóm 1 có C 3 1 . C 9 3 = 252 cách. Lúc đó còn lại 2 nữ, 6 nam, nhóm thứ 2 có C 2 1 . C 6 3 = 40 cách chọn. Cuối cùng còn 4 người là một nhóm: có 1 cách. Theo quy tắc nhân thì có: 252.440.1 = 10080 cách.
Vậy xác suất cần tìm là P = 10080 34650 = 16 55 .
CM
20 tháng 6 2018
Chọn A
Tổ có 12 người, chọn ra 4 người thì có 
cách
Còn lại 8 người, chọn tiếp ra 4 người thì có 
, còn lại 4 người là nhóm cuối.
Vậy không gian mẫu 
.
Chỉ có 3 nữ và chia mỗi nhóm có đúng 1 nữ và 3 nam.
Nhóm 1 có 
cách.
Lúc đó còn lại 2 nữ, 6 nam, nhóm thứ 2 có 
=40 cách chọn.
Cuối cùng còn 4 người là một nhóm: có 1 cách.
Theo quy tắc nhân thì có : 252.40.1= 10080 cách
Vậy xác suất cần tìm là
P = 
.
CM
21 tháng 4 2018
Gọi A: “mỗi nhóm có đúng một học sinh nữ”.
+) Số cách xếp 3 học sinh nữ vào 3 nhóm là 3! cách.
+) Chọn 3 học sinh nam cho nhóm thứ ba có 1 cách.
CM
14 tháng 3 2019
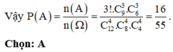
Đáp án D
Số cách chia tổ thành 3 nhóm đi làm 3 công việc khác nhau là C 12 4 . C 8 4 . C 4 4 = 34650
Với công việc thứ nhất có C 9 3 C 3 1 cách chọn 3 nam, 1 nữ.
Với công việc thứ nhất có C 6 3 C 2 1 cách chọn 3 nam, 1 nữ.
Với công việc thứ nhất có C 3 3 C 1 1 cách chọn 3 nam, 1 nữ.
Vậy xác suất cần tính là P = C 9 3 C 3 1 . C 6 3 C 2 1 . C 3 3 C 1 1 C 12 4 C 8 4 C 4 4 = 16 55
CM
21 tháng 10 2019
Chọn A
Lời giải. Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * )
Suy ra số học sinh nữ trong nhóm B là
25 - 9 - x - y = 16 - x - y
Khi đó, nhóm A có: 9 nam, x nữ và nhóm B có
y nam, 16 - x - y nữ
Xác suất để chọn được hai học sinh nam là
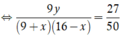
Mặt khác x + y < 16
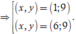
Vậy xác suất để chọn đươc hai học sinh nữ là
C 1 1 . C 6 1 C 10 1 . C 15 1 = 0 , 04
CM
2 tháng 1 2020
Đáp án B
Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * ) .
=> Số học sinh nữ trong nhóm B là 25 – 9 – x = 16 – x – y => x + y < 16
Khi đó, Nhóm A: 9 nam, x nữ và nhóm B: y nam, 16 – x – y nữ.
Xác suất để chọn được hai học sinh nam là
C 9 1 . C y 1 C 9 + x 1 . C 25 - 9 - x 1 = 0 , 54
⇔ 9 y ( 9 + x ) ( 16 - x ) = 27 50 .
⇒ y = 30 50 ( 9 + x ) ( 16 - x ) ⇒ x < 16 .
Vì y ∈ ℕ * ⇒ 3 50 ( 9 + x ) ( 16 - x ) ∈ N * .
=> (x, y) = {(1; 9), (6; 9), (11; 6)}.
Mặt khác x + y < 16
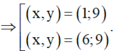
( Khi chia nhóm thì A,B có vai trò như nhau nên có 2 cặp thỏa mãn )
Vậy xác suất để chọn đươc hai học sinh nữ là 0,04.
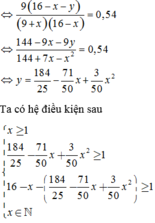
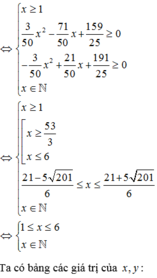
Không gian mẫu:
Chọn 5 người từ 15 người để lập nhóm 1 có \(C_{15}^5\) cách, chọn 5 người từ 10 người còn lại để lập nhóm 2 có \(C_{10}^5\) cách, tổ 3 có \(C_5^5\) cách
\(\Rightarrow C_{15}^5.C_{10}^5.C_5^5\) cách chọn bất kì
Bây giờ ta tính số cách chia sao cho có ít nhất 1 nhóm không có nữ:
Do 7 nữ luôn chia được vào ít nhất 2 nhóm sao cho mỗi nhóm có 5 người, do đó chỉ có nhiều nhất 1 nhóm (trong số 3 nhóm) chỉ toàn là nam.
Chọn 1 nhóm từ 3 nhóm để xếp 5 nam: \(C_3^1\) cách
Chọn 5 nam từ 8 nam để xếp vào nhóm nói trên: \(C_8^5\) cách
Còn 10 em xếp vào 2 nhóm còn lại: \(C_{10}^5.C_5^5\) cách
\(\Rightarrow C_3^1.C_8^5.C_{10}^5.C_5^5\) cách xếp sao cho có 1 ít nhất nhóm ko có nữ
\(\Rightarrow C_{15}^5.C_{10}^5.C_5^5-C_3^1.C_8^5.C_{10}^5.C_5^5\) cách xếp thỏa mãn
Xác suất: ...
Anh ơi! Câu này làm theo cách biến cố đối, hai học sinh nữ đứng cạnh nhau thì như nào ạ, em làm được trực tiếp còn làm gián tiếp không được ạ.
https://hoc24.vn/cau-hoi/doi-tuyen-hoc-sinh-gioi-cua-mot-truong-thpt-co-8-hoc-sinh-nam-va-4-hoc-sinh-nu-trong-buoi-le-trao-phan-thuong-cac-hoc-sinh-tren-duoc-xep-thanh-mot-hang-ngang-tinh-xac-suat-de-khi-xep-sao-cho-2-hoc.7929973126107