trên kệ sách có 4 quyển toán,3q lý,7q hoa a, Có bn cách xếp 3 loại sách vào giá sách b, Tính xác suất chọn được 5 quyển sao cho ít nhất 3 quyển hoá
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
Lấy ngẫu nhiên 3 quyển sách có: ![]() cách.
cách.
Gọi A là biến cố: 3 quyển được lấy ra có ít nhất một quyển toán.
Suy ra A ¯ là biến cố: lấy 3 quyển sách và không có quyển nào là quyển toán.
Khi đó ![]()
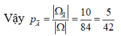
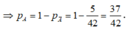

Đáp án C
Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản.
Lời giải:
Chọn 3 quyển sách trong 15 quyển sách có ![]() cách => n(Ω) = 455
cách => n(Ω) = 455
Gọi X là biến cố 3 quyển sách được lấy ra có ít nhất một quyển sách là toán.
Và X là biến cố 3 quyển sách được lấy ra không có quyển sách toán. Khi đó, ta xét các trường hợp sau:
TH1. Lấy được 2 quyển lý, 1 quyển hóa => có ![]() cách
cách
TH2. Lấy được 1 quyển lý, 2 quyển hóa => có ![]() cách
cách
TH3. Lấy được 3 quyển lý, 0 quyển hóa => có ![]() cách
cách
TH4. Lấy được 0 quyển lý, 3 quyển hóa => có ![]() cách
cách
Suy ra số phần tử của biến cố
X
là 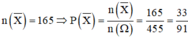
Vậy xác suất cần tính là ![]()

Đáp án C
Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản.
Lời giải:
Chọn 3 quyển sách trong 15 quyển sách có C 15 3 = 455 cách ⇒ n ( Ω ) = 455
Gọi X là biến cố 3 quyển sách được lấy ra có ít nhất một quyển sách là toán.
Và X là biến cố 3 quyển sách được lấy ra không có quyển sách toán. Khi đó, ta xét các trường hợp sau:
TH1. Lấy được 2 quyển lý, 1 quyển hóa => có C 5 2 . C 6 1 = 60 cách
TH2. Lấy được 1 quyển lý, 2 quyển hóa => có C 5 1 . C 6 2 = 75 cách
TH3. Lấy được 3 quyển lý, 0 quyển hóa => có C 5 3 . C 6 0 = 10 cách
TH4. Lấy được 0 quyển lý, 3 quyển hóa => có C 5 0 . C 6 3 = 20 cách
Suy ra số phần tử của biến cố X là
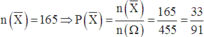
Vậy xác suất cần tính là
![]()

Đáp án C
Phương pháp.
Sử dụng định nghĩa của xác suất.
Lời giải chi tiết.
Tổng số sách là 4 + 3 + 2 = 9. Số cách lấy 3 quyển sách là C 9 3 = 84 (cách).
Số quyển sách không phải là sách toán là 3 + 2 = 5
Số cách lấy 3 quyển sách không phải là sách toán là C 5 3 = 10 (cách).
Do đó số cách lấy được ít nhất một quyển sách toán là 84 - 10 = 74 (cách).
Vậy xác suất để lấy đượcc ít nhất một quyển là toán là 74 84 = 37 42

Đáp án C
Lấy ngẫu nhiên 3 cuốn sách có: C 9 3 = 84 cách
Gọi A là biến cố: Lấy 3 cuốn sách và không có cuốn nào là cuốn toán
Suy ra A ¯ là biến cố: 3 quyển được lấy ra có ít nhất một quyển là toán
Khi đó Ω A = C 5 3 = 10 .
Vậy p A = Ω A Ω = 10 84 = 5 42 ⇒ p A ¯ = 1 − p A = 37 42

Đáp án C
Lấy ngẫu nhiên 3 cuốn sách có: C 9 3 = 84 cách
Gọi A là biến cố:
Lấy 3 cuốn sách và không có cuốn nào là cuốn toán
Suy ra A ¯ là biến cố:
3 quyển được lấy ra có ít nhất một quyển là toán
Khi đó Ω A = C 5 3 = 10
Vậy P A = Ω A Ω = 5 42
⇒
p
A
¯
=
1
-
p
A
=
37
42

Số cách chọn 3 quyển sách văn là \(C^3_4=4\).
Số cách chọn 3 quyển sách anh là \(C^3_5=10\).
a, Số cách sắp xếp vào 1 kệ dài là \(9!.4.10=14515200\) cách.
b, Coi số sách mỗi loại là một phần tử.
Số cách sắp xếp thỏa mãn yêu cầu bài toán là \(3!.4.10=240\) cách.


a. Có bao nhiêu cách xếp 3 loại sách vào giá sách?
Để tính số cách xếp 3 loại sách vào giá sách, ta sử dụng công thức tổ hợp chập 3 của 3 số 4, 3 và 7 (vì có 3 loại sách là toán, lý và hoá):
C(4,3) * C(3,3) * C(7,3) = 4 * 1 * 35 = 140
Vậy có 140 cách xếp 3 loại sách vào giá sách.
b. Tính xác suất chọn được 5 quyển sao cho ít nhất 3 quyển hoá.
Để tính xác suất chọn được ít nhất 3 quyển hoá trong 5 quyển, ta phải tính tổng xác suất chọn được 3 quyển, 4 quyển hoặc 5 quyển hoá.
Xác suất chọn được 3 quyển hoá:
C(7,3) * C(7,2) / C(14,5) = 35 * 21 / 2002 = 0,372
Giải thích: Để chọn được 3 quyển hoá, ta chọn 3 quyển hoá từ 7 quyển hoá và chọn 2 quyển từ 7 quyển còn lại (toán và lý). Tổng số cách chọn 5 quyển là C(14,5).
Xác suất chọn được 4 quyển hoá:
C(7,4) * C(4,1) / C(14,5) = 35 * 4 / 2002 = 0,070
Giải thích: Để chọn được 4 quyển hoá, ta chọn 4 quyển hoá từ 7 quyển hoá và chọn 1 quyển từ 4 quyển toán và lý còn lại. Tổng số cách chọn 5 quyển là C(14,5).
Xác suất chọn được 5 quyển hoá:
C(7,5) / C(14,5) = 21 / 2002 = 0,010
Giải thích: Để chọn được 5 quyển hoá, ta chọn 5 quyển hoá từ 7 quyển hoá. Tổng số cách chọn 5 quyển là C(14,5).
Vậy, tổng xác suất chọn được ít nhất 3 quyển hoá trong 5 quyển là:
0,372 + 0,070 + 0,010 = 0,452
Vậy, xác suất chọn được ít nhất 3 quyển hoá trong 5 quyển là 0,452 (hoặc khoảng 45,2%).