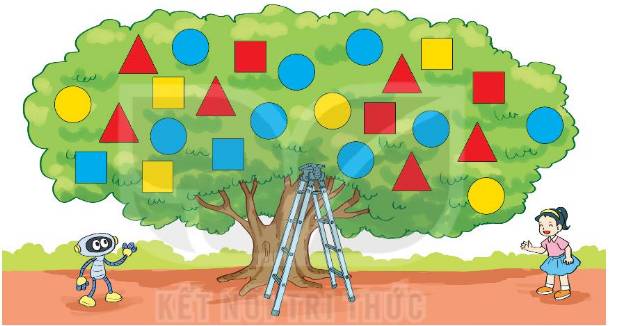
Rô-bốt cắt giấy màu được các hình gồm hình vuông, hình tròn, hình tam giác rồi trang trí lên cây như hình vẽ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.

c) Hình hộp chữ nhật ở Hình 2 có 6 mặt , 12 cạnh, 8 đỉnh.

Chiều dài đèn nháy có độ dài là:
25 + 25 + 60 + 40 = 150 (cm)
Đáp số: 150 cm

Hình ban đầu có độ dài 1 cạnh là 5 ô vuông.
Do đó để hình đó là hình vuông thì các cạnh còn lại cũng là 5 ô vuông thì Rô-bốt cần cắt theo đoạn thẳng MN.
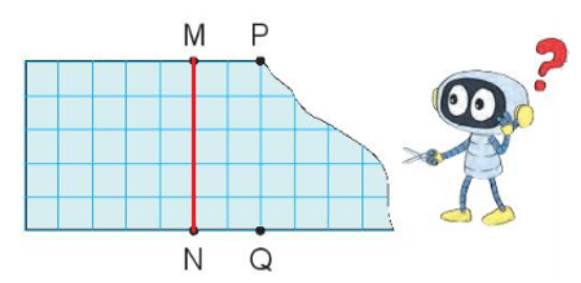
Vậy để cắt tờ giấy như hình bên thành một hình vuông, Rô-bốt cần cắt theo đoạn thẳng MN.
Chọn đáp án D.

Em có dãy số: 1000; 2000; 3000; 4000; 5000; 6000; 7000; 8000; 9000
Các số điền vào dấu “?” theo thứ tự từ trái sang phải lần lượt là:
4000; 5000; 7000; 8000; 9000

Giả sử các hình tròn bán kính \({R_1} = R,{R_2} = \frac{R}{2},{R_3} = \frac{R}{4} = \frac{R}{{{2^2}}},...,{R_n} = \frac{R}{{{2^{n - 1}}}},...\) có diện tích lần lượt là \({u_1},{u_2},{u_3},...,{u_n},...\) Ta có:
\(\begin{array}{l}{u_1} = \pi R_1^2 = \pi {R^2},{u_2} = \pi R_2^2 = \pi {\left( {\frac{R}{2}} \right)^2} = \pi {R^2}.\frac{1}{{{2^2}}},{u_3} = \pi R_3^2 = \pi {\left( {\frac{R}{{{2^2}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^4}}},...,\\{u_n} = \pi R_n^2 = \pi {\left( {\frac{R}{{{2^{n - 1}}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^{2n - 2}}}},...\end{array}\)
\(\begin{array}{l}S = {u_1} + {u_2} + ... + {u_n} + ... = \pi {R^2} + 2\pi {R^2}.\frac{1}{{{2^2}}} + 4.\pi {R^2}.\frac{1}{{{2^4}}} + ... + {2^{n + 1}}\pi {R^2}.\frac{1}{{{2^{2n - 2}}}} + ...\\\,\,\,\, = \pi {R^2} + \pi {R^2}.\frac{1}{2} + \pi {R^2}.\frac{1}{{{2^2}}} + ... + \pi {R^2}.\frac{1}{{{2^{n - 1}}}} + ...\\\,\,\,\, = \pi {R^2}\left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...} \right)\end{array}\)
Xét tổng: \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...\)
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\) và công bội \(q = \frac{1}{2}\) nên: \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ... = \frac{1}{{1 - \frac{1}{2}}} = 2\).
Vậy \(S = \pi {R^2}.{S_n} = 2\pi {R^2}\).

Ta có V 1 = a 3 16 và V 2 = a . 1 2 . a 3 . 3 2 . a 3 = a 3 3 36 .
Do đó V 1 > V 2
Đáp án A