cho da thuc P(x)=ax+b. Tìm điều kiện của a và b để P(x1+x2)=P(x1)+P(x2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
0
NH
9 tháng 6 2020
Ta có: P(x1 + x2) = a(x1 + x2) + b = ax1 + ax2 + b
P(x1) + P(x2) = ax1 + b + ax2 + b = ax1 + ax2 + 2b
Để P(x1 + x2) = P(x1) + P(x2) thì ax1 + ax2 + b = ax1 + ax2 + 2b
=> b = 2b => b - 2b = 0 => -b = 0 => b = 0
Vậy khi b = 0 , a 
TT
0
TT
1
22 tháng 3 2022
\(f\left(x_1+x_2\right)=f\left(x_1\right)+f\left(x_2\right)\)
\(\Rightarrow a\left(x_1+x_2\right)+b=ax_1+b+ax_2+b\)
\(\Rightarrow a\left(x_1+x_2\right)+b=a\left(x_1+x_2\right)+2b\)
\(\Rightarrow b=2b\)
\(\Rightarrow2b-b=0\Rightarrow b=0\)
TT
0
11 tháng 5 2021
\(x^2+ax+b+1=0\)
\(\Delta=a^2-4b-4\)
Để pt có 2 nghiệm pb \(\Leftrightarrow\Delta>0\Leftrightarrow a^2-4b-4>0\)
Theo hệ thức Vi-et ta có: \(\hept{\begin{cases}x_1+x_2=-a\\x_1.x_2=b+1\end{cases}}\)
Ta có: \(\hept{\begin{cases}x_1-x_2=3\\x_1^3-x_2^3=9\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1-x_2=3\\\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)=9\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1-x_2=3\\x_1^2+x_1x_2+x_2^2=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1-x_2=3\\\left(x_1-x_2\right)^2+3x_1x_2=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1-x_2=3\\x_1x_2=-2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1=3+x_2\\\left(3+x_2\right)x_2=-2\left(1\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow x_2^2+3x_2+2=0\)
\(\Delta=1\)
\(\Rightarrow\)pt có 2 nghiệm pb \(\orbr{\begin{cases}x_2=\frac{-3+1}{2}=-1\Rightarrow x_1=2\\x_2=\frac{-3-1}{2}=-2\Rightarrow x_1=1\end{cases}}\)
TH1: \(x_1=2;x_2=-1\)
\(\Rightarrow\hept{\begin{cases}a=-1\\b=-3\end{cases}}\)( LOẠI vì a^2 -4b-4 <0 )
TH2: \(x_1=1;x_2=-2\)
\(\Rightarrow\hept{\begin{cases}a=1\\b=-3\end{cases}}\)( tm )
VẬY ...
29 tháng 7 2023
a: Để phương trình có nghiệm thì (-2)^2-4(m-3)>=0
=>4-4m+12>=0
=>-4m+16>=0
=>-4m>=-16
=>m<=4
b: x1-x2=4
x1+x2=2
=>x1=3; x2=-1
x1*x2=m-3
=>m-3=-3
=>m=0(nhận)
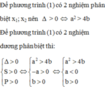
Ta có :
\(P\left(x_1+x_2\right)=a.\left(x_1+x_2\right)+b\)
\(P\left(x_1\right)+P\left(x_2\right)=a.x_1+b+a.x_2+b=a\left(x_1+x_2\right)+2b\)
Theo đề bài ta có \(a\left(x_1+x_2\right)+b=a\left(x_1+x_2\right)+2b\). Lấy VP - VT, ta được b = 0
Như vậy với b = 0 và mọi số thực A thì \(P\left(x_1+x_2\right)=P\left(x_1\right)+P\left(x_2\right)\)