Giúp e với ạaaa hleppppppp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
20 tháng 3 2022
Lời giải:
a. Để $f(x)=x^2-2mx+3m+4\geq 0$ với mọi $x\in\mathbb{R}$ thì:
\(\left\{\begin{matrix}
a=1>0\\
\Delta'=m^2-3m-4\leq 0\end{matrix}\right.\Leftrightarrow m^2-3m-4\leq 0\)
$\Leftrightarrow (m+1)(m-4)\leq 0$
$\Leftrightarrow -1\leq m\leq 4$
b.
Để pt có 2 nghiệm pb cùng dấu thì:
\(\left\{\begin{matrix}
\Delta'=m^2-3m-4>0\\
P=3m+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
(m+1)(m-4)> 0\\
m> \frac{-4}{3}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
m> 4 \text{hoặc} m< -1\\
m> \frac{-4}{3}\end{matrix}\right.\)
$\Leftrightarrow m>4$ hoặc $\frac{-4}{3}< m < -1$
AH
Akai Haruma
Giáo viên
20 tháng 3 2022
Lời giải:
a. Để $f(x)=x^2-2mx+3m+4\geq 0$ với mọi $x\in\mathbb{R}$ thì:
\(\left\{\begin{matrix}
a=1>0\\
\Delta'=m^2-3m-4\leq 0\end{matrix}\right.\Leftrightarrow m^2-3m-4\leq 0\)
$\Leftrightarrow (m+1)(m-4)\leq 0$
$\Leftrightarrow -1\leq m\leq 4$
b.
Để pt có 2 nghiệm pb cùng dấu thì:
\(\left\{\begin{matrix}
\Delta'=m^2-3m-4>0\\
P=3m+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
(m+1)(m-4)> 0\\
m> \frac{-4}{3}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
m> 4 \text{hoặc} m< -1\\
m> \frac{-4}{3}\end{matrix}\right.\)
$\Leftrightarrow m>4$ hoặc $\frac{-4}{3}< m < -1$
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2022
Gọi chữ số hàng chục là x và chữ số hàng đơn vị là y (x;y là các chữ số từ 0 đến 9)
Do chữ số hàng chục hơn chữ số hàng đơn vị là 4
\(\Rightarrow x-y=4\)
Giá trị chữ số ban đầu: \(10x+y\)
Giá trị chữ số sau khi đổi chỗ: \(10y+x\)
Do tổng số mới và số cũ là 132 nên ta có pt:
\(10x+y+10y+x=132\Rightarrow11\left(x+y\right)=132\Rightarrow x+y=12\)
Ta được hệ: \(\left\{{}\begin{matrix}x-y=4\\x+y=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=8\\y=4\end{matrix}\right.\)
Vậy số đó là 84
14 tháng 4 2023
Gọi số học sinh nam và số học sinh nữ lần lượt là a,b
Theo đề, ta có: a+b=46 và 2a+3b=118
=>a=20 và b=26
13 tháng 4 2023
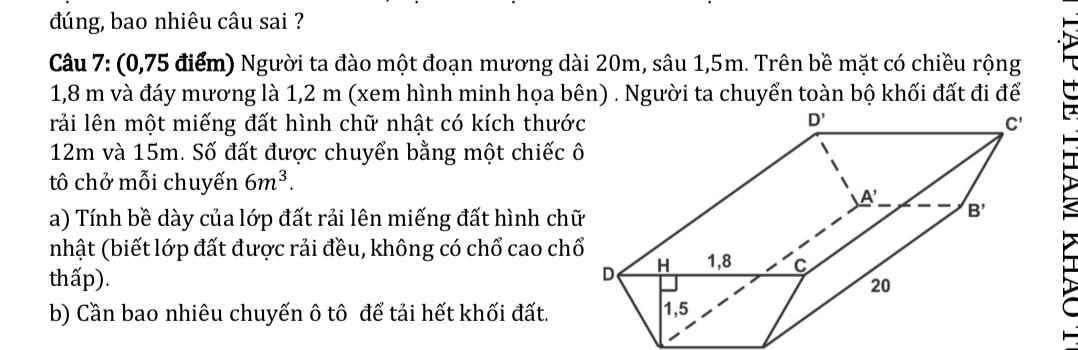
a: Phần đất đào lên là một hình lăng trụ đứng. Mặt đáy của hình lăng trụ đứng là hình thang có các cạnh đáy là 1,8m và 1,2m, chiều cao là 1,5m
Chiều cao là 20m
\(S_{đáy}=\dfrac{1.8+1.2}{2}\cdot1.5=1.5\cdot1,5=2.25\left(m^2\right)\)
Thể tích khối đất phải đào lên là:
2,25*20=40,5(m3)
Bề dày của lớp đất rải là:
40,5:20:1,5=27:20=1,35(m)
b: Số chuyến ô tô phải dùng là:
40,5:6=6,75
=>Cần 7 chuyến
KB
3
AH
Akai Haruma
Giáo viên
17 tháng 7 2021
a.
$2\sqrt{3}-\sqrt{x^2+4}=0$
$\Leftrightarrow 2\sqrt{3}=\sqrt{x^2+4}$
$\Leftrightarrow 12=x^2+4$
$\Leftrightarrow 8=x^2$
$\Leftrightarrow x=\pm 2\sqrt{2}$
b. ĐKXĐ: $x\geq -1$
$\sqrt{16(x+1)}-\sqrt{9(x+1)}=1$
$\Leftrightarrow 4\sqrt{x+1}-3\sqrt{x+1}=1$
$\Leftrightarrow \sqrt{x+1}=1$
$\Leftrightarrow x+1=1$
$\Leftrightarrow x=0$ (tm)
c. ĐKXĐ: $x\geq 0$
$3\sqrt{2x}+5\sqrt{8x}-20-\sqrt{18x}=0$
$\Leftrightarrow 3\sqrt{2x}+10\sqrt{2x}-20-3\sqrt{2x}=0$
$\Leftrightarrow 10\sqrt{2x}-20=0$
$\Leftrightarrow \sqrt{2x}=2$
$\Leftrightarrow 2x=4$
$\Leftrightarrow x=2$ (tm)
AH
Akai Haruma
Giáo viên
17 tháng 7 2021
d.
PT \(\Rightarrow \left\{\begin{matrix} x-1\geq 0\\ x^2-\sqrt{8x}+2=(x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x=\frac{1+\sqrt{2}}{2}\end{matrix}\right.\Leftrightarrow x=\frac{1+\sqrt{2}}{2}\)
e. ĐKXĐ: $x\leq 1$
PT $\Leftrightarrow \sqrt{1-x}+2\sqrt{1-x}-\frac{4}{3}\sqrt{1-x}+5=0$
$\Leftrightarrow \frac{5}{3}\sqrt{1-x}=-5< 0$ (vô lý)
Vậy pt vô nghiệm.
f. ĐKXĐ: $x\geq -1$
PT $\Leftrightarrow 2\sqrt{(\sqrt{x+1}+1)^2}-\sqrt{x+1}=4$
$\Leftrightarrow 2(\sqrt{x+1}+1)-\sqrt{x+1}=4$
$\Leftrightarrow \sqrt{x+1}=2$
$\Leftrightarrow x=3$ (tm)
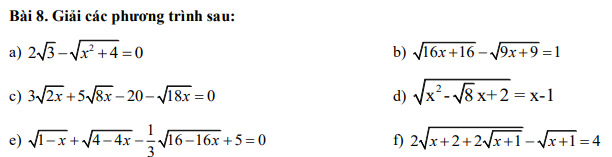
Gọi giao của AO với (O) là D
=>AD=2R
ΔACD nội tiếp đường tròn đường kính AD
=>ΔACD vuông tại C
mà CB vuông góc AD
nên CB^2=AB*BD
=>CB^2=AB(2*R-AB)
=>1,1(2*R-1,1)=28,4^2
=>R=367,2m
=>AD=734,4(m)
\(AC=\sqrt{1.1^2+28.4^2}=28,42\left(m\right)\)
OA=OC=367,2m
\(cosAOC=\dfrac{OA^2+OC^2-AC^2}{2\cdot OA\cdot OC}\simeq0.998\)
=>góc AOC=4 độ
=>sđ cung AC=4 độ