Giúp e với ạ
Bài IV (3 điểm) Cho đường tròn (O;R) và dường thẳng d không có điểm chung với dương trên. Gọi M là một điểm thuộc đường thẳng d. Qua M kẻ hai tiếp tuyến MA, MB tôi đường tròn. Gọi II là lính chiếu vuông góc của 0 trên đường thẳng d 1) Chứng minh tứ giác OAMI nội tiếp.
2) Gọi giáo diễm của AB với OII và OM lần lượt tại K và l Chứng minh OK. OFF OLOM
1) Đoạn thẳng GM của...
Đọc tiếp
Giúp e với ạ Bài IV (3 điểm) Cho đường tròn (O;R) và dường thẳng d không có điểm chung với dương trên. Gọi M là một điểm thuộc đường thẳng d. Qua M kẻ hai tiếp tuyến MA, MB tôi đường tròn. Gọi II là lính chiếu vuông góc của 0 trên đường thẳng d 1) Chứng minh tứ giác OAMI nội tiếp. 2) Gọi giáo diễm của AB với OII và OM lần lượt tại K và l Chứng minh OK. OFF OLOM 1) Đoạn thẳng GM của (O) tại E. Chứng minh I là tâm đường trên nội tiếp tam giá MAD. Tín vị trí điểm M trên đường thẳng d để diện tích tam giác OJK đạt giá trị lớn nhất.
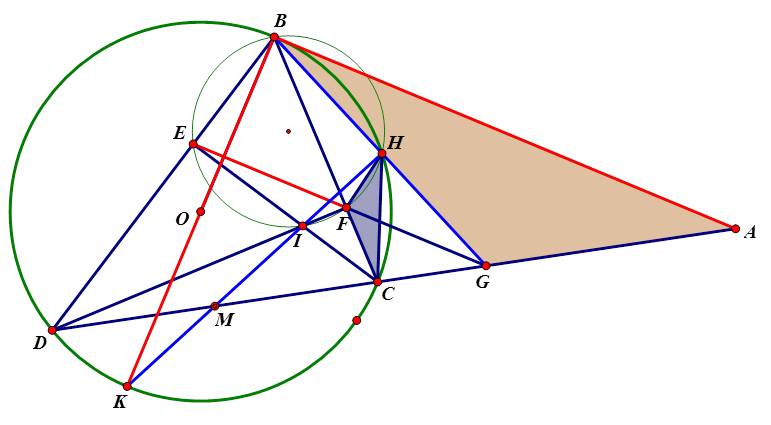
1: góc OAM=góc OIM=90 độ
=>OAIM nội tiếp
2: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại I
Xét ΔOFK vuông tại F và ΔOIM vuông tại I có
góc FOK chung
=>ΔOFK đồng dạng với ΔOIM
=>OF/OI=OK/OM
=>OF*OM=OI*OK