Cho đoạn thẳng AB và N là trung điểm của AB . Lấy M nằm giữa N và B . CMR : MN=(AM-BM):2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 4 2018
Từ giả thiết AB = 12cm và điểm N nằm giữa hai điểm A, B sao cho AN = 2cm
Suy ra: AN + NB = AB
Thay số 2 + NB = 12 nên NB = 10 cm
M là trung điểm của đoạn thẳng BN nên BM = MN = 5cm.
Cũng do MN = 5cm và P là trung điểm của đoạn thẳng MN nên NP = PM = 2,5cm. Từ đó, ta có thể vẽ được hình như sau
* Trên tia NB có NP < NB (do 2,5cm < 10cm) nên điểm P nằm giữa hai điểm N và B.
Do đó: BN = NP + BP
Suy ra BP = BN - NP = 10 - 2,5 = 7,5 cm
CM
7 tháng 3 2017
Theo giả thiết ta vẽ được hình:
Khi đó AN = AM + MN và AB = AN + NB.
Suy ra AB = (AM + MN) + NB
Do AM = NB = 2 cm nên 10 = 2 + MN + 2.
Từ đó tính được MN = 10 - 4 = 6 (cm)
19 tháng 12 2020
Theo đầu bài cho trên tia AB nghĩa là lấy A làm gốc,lấy điểm M,N để AM=3cm,AN=6cm có thể suy ra M nằm giữa A,N.
MN=AN-AM=6-3=3cm
NB=AB-AN=8-6=2cm
vậy MN=3cm,NB=2cm
Theo phần đầu M nằm giữa A,N.mà AM=MN=3cm vậy M nằm giữa và cách đều A,N.Vậy M là trung điểm của AN
CM
18 tháng 3 2017
Câu đúng: e), f), g).
Câu sai: a), b), c), d).
Điểm M được gọi là trung điểm của đoạn thẳng AB nếu M nằm giữa A, B và cách đều hai điểm đó (AM = MB).
* Câu a còn thiếu điều kiện là MA = MB.
* Câu b sai vì thiếu điều kiện M nằm giữa A và B.
* Câu c thiếu điều kiện MA = MB.
* Câu d thiếu điều kiện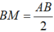 
4 tháng 11 2019
a, xét tam giác MAO và tam giác NBO có :
MO = ON do O là trung điểm của MN (gt)
góc OMa = góc ONB (gt)
MA = BN (gt)
=> tam giác MAO = tam giác NBO (c-g-c)
=> AO = OB (Đn)
mà O nằm giữa A và B
=> O là trung điểm của AB (đn)
b, góc OMa = góc ONb (gt)
=> Ma // Nb (đl)
=> góc CAB = góc ABD (đl)
xét tam giác CAB = tam giác DBA có : AC = BD (gt)
AB chung
=> tam giác CAB = tam giác DBA (c-g-c)
=> BC = AD (đn)
27 tháng 11 2015
A-----------M----------C-----N-----B
M là trung điểm AC => MC = MA =AC/2
N là trung điểm BC => NC = NB = CB/2
=>MC + NC = (AC+CB)/2 => MN =AB//2 => AB = 2MN =2.3 =6