Bài tập 2: Cho AABC nhọn nội tiếp đường tròn (O; R). Vẽ hai đường cao BE và CF của tam giác cát nhau tại I. a/ Chứng minh tứ giác AEIF nội tiếp. b/ Hai đường thẳng BE và CF cắt đường tròn lần lượt tại P và Q. Chứng minh BPQ = BCQ,
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
15 tháng 5 2023
(a) + Ta có : \(OB=OC=R\Rightarrow O\) thuộc đường trung trực của \(BC.\)
Do \(I\) là tâm đường tròn nội tiếp \(\Delta ABC\) nên \(AI\) hay \(AD\) là đường phân giác của
\(\hat{BAC}\Rightarrow\hat{BAD}=\hat{DAC}\Rightarrow\stackrel\frown{BD}=\stackrel\frown{CD}\) (các góc nội tiếp bằng nhau chắn các cung bằng nhau) \(\Rightarrow BD=CD\Rightarrow D\) thuộc đường trung trực của \(BC\).
Từ đó, suy ra \(OD\) là đường trung trực của \(BC\Rightarrow OD\perp BC\) (đpcm).
+ Ta có : \(\hat{DBC}=\hat{DAC}=\hat{BAD}\) (hai góc nội tiếp cùng chắn cung \(CD\) và chứng minh trên). Mà : \(\hat{ABI}=\hat{IBC}\) (do \(I\) là tâm đường tròn nội tiếp \(\Delta ABC\Rightarrow BI\) là phân giác của \(\hat{ABC}\)).
Ta sẽ có được : \(\hat{DBC}+\hat{IBC}=\hat{BAD}+\hat{ABI}\)
\(\Leftrightarrow\hat{IBD}=\hat{BID}\) (\(\hat{BID}\) là góc ngoài của \(\Delta ABI\))
\(\Rightarrow\Delta IBD\) cân tại \(D\) (đpcm).
(b) Xét \(\Delta PAD,\Delta DTR:\) \(\left\{{}\begin{matrix}\hat{PDA}=\hat{TDR}=90^o\left(gt\right)\\\hat{PAD}=\hat{DRT}\end{matrix}\right.\) (cùng phụ với \(\hat{HTA}=\hat{DTR}\) (đối đỉnh))
\(\Rightarrow\Delta PAD\sim\Delta DTR\left(g.g\right)\Leftrightarrow\dfrac{PD}{DT}=\dfrac{AD}{DR}\Leftrightarrow DT.DA=PD.DR\left(1\right).\)
Xét \(\Delta DBT,\Delta DAB:\left\{{}\begin{matrix}\hat{ADB}\text{ chung}\\\hat{DBT}=\hat{DAB}\left(=\hat{BAD}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta DBT\sim\Delta DAB\left(g.g\right)\Leftrightarrow\dfrac{DT}{DB}=\dfrac{DB}{DA}\Leftrightarrow DB^2=DT.DA\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow PD.DR=DB^2=DI^2\) (\(\Delta IDB\) cân tại \(D\left(cmt\right)\Rightarrow DB=DI\)) \(\Leftrightarrow\dfrac{PD}{DI}=\dfrac{DI}{DR}\).
Xét \(\Delta PDI,\Delta IDR:\left\{{}\begin{matrix}\dfrac{PD}{DI}=\dfrac{DI}{DR}\left(cmt\right)\\\hat{PDI}=\hat{IDR}=90^o\end{matrix}\right.\)
\(\Rightarrow\Delta PDI\sim\Delta IDR\left(c.g.c\right)\Leftrightarrow\hat{IPD}=\hat{DIR}\).
Lại có trong \(\Delta IDP\) vuông tại \(D\) : \(\hat{IPD}+\hat{PID}=90^o\) (hai góc phụ nhau), suy ra : \(\hat{DIR}+\hat{PID}=90^o=\hat{PIR}\)
Vậy : \(IP\perp IR\) (đpcm).
TM
15 tháng 5 2023
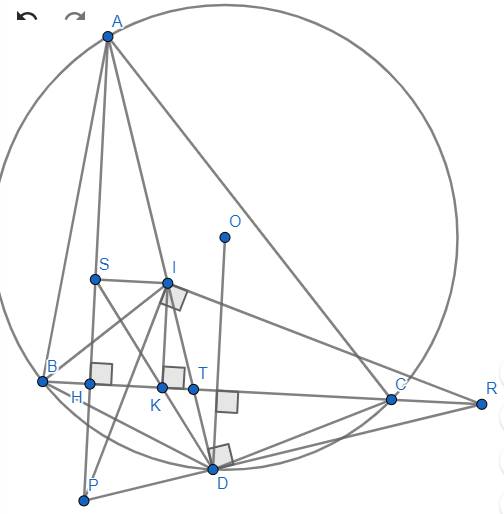
(c) Do \(\left\{{}\begin{matrix}IK\perp BC\\AH\perp BC\end{matrix}\right.\left(gt\right)\Rightarrow IK\left|\right|AH\Rightarrow\dfrac{DI}{DA}=\dfrac{DK}{DS}\) (hệ quả của định lí Ta-lét) \(\Rightarrow\dfrac{DB}{DA}=\dfrac{DK}{DS}\). (do \(\Delta IBD\) cân tại \(D\left(cmt\right)\) nên \(ID=DB\)).
Ta cũng có ở câu (b) : \(\Delta DBT\sim\Delta DAB\left(g.g\right)\Rightarrow\dfrac{DB}{DA}=\dfrac{DT}{DB}=\dfrac{DT}{DI}\).
Từ hai điều trên suy ra : \(\dfrac{DK}{DS}=\dfrac{DT}{DI}\).
Xét \(\Delta DKT,\Delta DSI:\left\{{}\begin{matrix}\dfrac{DK}{DS}=\dfrac{DT}{DI}\left(cmt\right)\\\hat{D}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta DKS\sim\Delta DSI\left(c.g.c\right)\Rightarrow\hat{DKT}=\hat{DSI}\). Hai góc này ở vị trí đồng vị nên \(TK\left|\right|SI\) hay \(BC\left|\right|SI\).
Ta lại có : \(AH\perp BC\Rightarrow SI\perp AH\Rightarrow\hat{PSI}=90^o.\)
Xét tứ giác \(SIDP:\hat{PSI}+\hat{PDI}=90^o+90^o=180^o\). Đây là hai góc đối nhau, vì vậy, tứ giác \(SIDP\) nội tiếp được một đường tròn (đpcm).
5 tháng 6 2023
Không thấy câu a) của bạn đâu nên mình chứng minh câu b) luôn nhé.
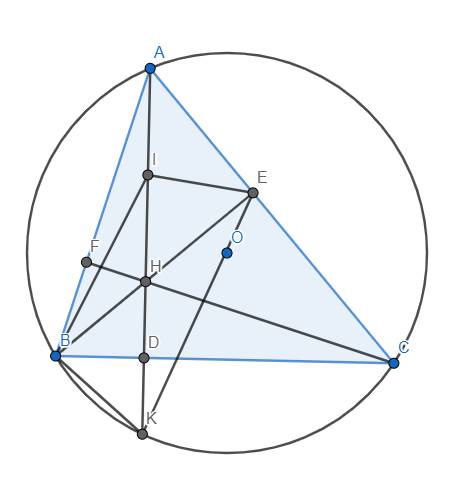
Dễ thấy \(\widehat{BHD}=\widehat{BCA}\) vì cùng phụ với \(\widehat{HBC}\).
Lại có \(\widehat{BKD}=\widehat{BKA}=\widehat{BCA}\) nên suy ra \(\widehat{BHD}=\widehat{BKD}\) hay \(\widehat{BHK}=\widehat{BKI}\).
Mặt khác, tam giác AEH vuông tại E có trung tuyến EI nên \(EI=\dfrac{AH}{2}=IH\) \(\Rightarrow\Delta IEH\) cân tại I \(\Rightarrow\widehat{IHE}=\widehat{IEH}=\widehat{IEB}\)
Mà \(\widehat{IHE}=\widehat{BHK}=\widehat{BKI}\) \(\Rightarrow\widehat{IEB}=\widehat{IKB}\), từ đó suy ra tứ giác IEKB nội tiếp. (đpcm)
17 tháng 4 2023
a: góc ACF=1/2*sđ cung AF
góc BCF=1/2*sđ cung BF
góc ACF=góc BCF
=>AF=BF
mà OA=OB
nên OF là trung trực của AB
=>OF vuông góc BA tại M
góc ABE=1/2*sđ cung AE
góc CBE=1/2*sđ cung CE
góc ABE=góc CBE
=>AE=CE
mà OA=OC
nên OE là trung trực của AC
=>OE vuông góc AC tại N
b: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
23 tháng 1 2020
1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )
LL
11 tháng 4 2022
a. Vì I là trung điểm của AC \(\Rightarrow\) OI \(\perp\) AC ( quan hệ giữa đk và dây )
hay KI \(\perp\) AC
Xét tứ giác CIKH có: góc KIC + góc KHC = 90o + 90o = 180o ( tổng 2 góc đối = 180o )
\(\Rightarrow\) tứ giác CIKH nội tiếp ( đpcm )
b. Ta có: góc CBD = góc CAD ( 2 góc nội tiếp cùng chắn cung DC ) (1)
Xét \(\Delta\) AKC có: KI là đường trung tuyến đồng thời là đường cao
\(\Rightarrow\) \(\Delta\) AKC là tam giác cân tại K \(\Rightarrow\) góc CAK = góc ACK
hay góc CAD = góc ACK (2)
Từ (1), (2) \(\Rightarrow\) góc ACK = góc CBD ( đpcm )
a: góc AEI+góc AFI=180 độ
=>AEIF nội tiếp
b: Xét (O) có
góc BPQ=1/2*sđ cung BQ
góc BCQ=1/2*sđ cug BQ
=>góc BPQ=góc BCQ