tìm xác suất để 2 người gặp ngẫu nhiên ngoài đường trùng sinh nhâtj nhau . (giả sử 1 năm 365)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Không gian mẫu: \(365.365=365^2\)
Người thứ nhất có 365 khả năng ngày sinh, người thứ 2 chỉ có 1 khả năng trùng với người thứ nhất nên có \(365.1=365\) khả năng 2 người trùng ngày sinh
Xác suất: \(P=\dfrac{365}{365^2}=\dfrac{1}{365}\)

Đáp án B.
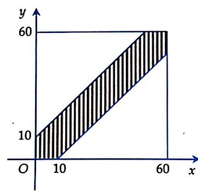
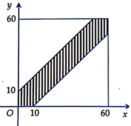
Gọi x (phút) là thời gian mà bạn A đến chờ ở thư viện.
Gọi y (phút) là thời gian mà bạn B đến chờ ở thư viện.
Điều kiện: ![]()
![]() (là diện tích hình vuông cạnh 60)
(là diện tích hình vuông cạnh 60)
Điều kiện gặp nhau là
![]() (*)
(*)
Do điểm ![]() thỏa điều kiện (*) thuộc lục giác gạch sọc giới hạn bởi 2 đường thẳng
thỏa điều kiện (*) thuộc lục giác gạch sọc giới hạn bởi 2 đường thẳng ![]() là hình vuông của không gian mẫu.
là hình vuông của không gian mẫu.
Lục giác có diện tích
![]()
Vậy xác suất để 2 người gặp nhau là:
![]()

Chọn C
Ta có: ![]()
Gọi A là biến cố “trong 3 người được chọn đó không có 2 người ngồi kề nhau”
=> A ¯ là biến cố “trong 3 người đươc chọn có ít nhất 2 người ngồi kề nhau”
![]()

TH 1: 3 người ngồi kề nhau có 13 cách chọn.
TH 2: có 2 người ngồi cạnh nhau
- Hai người ngồi cạnh nhau ngồi đầu hàng có 2 cách chọn, với mỗi cách chọn như vậy có 12 cách chọn người còn lại vậy có: 2.12=24 cách.
- Hai người ngồi cạnh nhau không ngồi đầu hàng có 12 cách chọn, với mỗi cách chọn như vậy có 11 cách chọn người còn lại vậy có: 11.12=132 cách.
![]()

n(Ω) = \(C_{40}^4=91390\)
Kí hiệu A : "giáo viên gặp được lớp trưởng "
B : " giáo viên gặp được bí thư chi đoàn"
C : " giáo viên gặp được thủ quỹ "
D : " giáo viên gặp được lớp phó "
=> P(A) = P(B) = P(C) = P(D) = \(\dfrac{C_4^1}{C_{40}^4}\) ~ 0,00004
a) Cần tính \(P\left(A\cap B\right)\) = P(A) . P(B) = 0,000042
b) Cần tính \(P\left(\left(A\cap D\right)\cup\left(A\cap C\right)\right)\\ =P\left(A\cap D\right)+P\left(A\cap C\right)-P\left(A\cap D\right).P\left(A\cap C\right)\\ =P\left(A\right).P\left(D\right)+P\left(C\right).P\left(A\right)-P\left(A\right).P\left(D\right).P\left(A\right).P\left(C\right)\\ =2P^2\left(A\right)-P^4\left(A\right)\\ \)
c) cần tính \(P\left(A\right).P\left(B\right).P\left(D\right).\left(1-P\left(C\right)\right)\)

Không gian mẫu: \(C_{40}^4\)
a. Số cách thỏa mãn: \(1.1.C_{38}^2=C_{38}^2\)
Xác suất: \(P=\dfrac{C_{38}^2}{C_{40}^4}\)
b. Số cách thỏa mãn: \(1.2.C_{37}^2\)
Xác suất: \(\dfrac{2.C_{37}^2}{C_{40}^4}\)
c. Số cách: \(1.1.1.C_{36}^1=36\)
Xác suất: \(\dfrac{36}{C_{40}^4}\)
Câu c:
Chọn lớp trưởng: có 1 cách
Chọn bí thư đoàn: có 1 cách
Chọn lớp phó học tập: có 1 cách
Còn lại 37 học sinh, nhưng loại trừ đi thủ quỹ nên chỉ còn 36
Chọn 1 bạn còn lại trong 36 bạn này: \(C_{36}^1\) cách
Theo quy tắc nhân ta có số cách thỏa mãn: \(1.1.1.C_{36}^1\)








Biến cố đối là hai người này có ngày sinh khác nhau
=>Xác suất của biến cố là: \(1-\dfrac{364\cdot365}{365^2}=1-\dfrac{364}{365}=\dfrac{1}{365}\)