Cho tam giác ABC vuông tại A, AD là phân giác \(\widehat{BAC}\) ( D ∈ BC ). Gọi N là hình chiếu vuông góc của D trên AC và M là hình chiếu vuông góc của D trên AB.
1> Tứ giác AMDN là hình gì? Tại sao?
2> Cho AB = 3cm ; AC = 4cm . Tính BD, DC và diện tích tứ giác AMDN
3> MC cắt AD tại I và cắt DN tại K. Chứng minh rằng \(\dfrac{1}{MI}=\dfrac{1}{MK}+\dfrac{1}{MC}\)

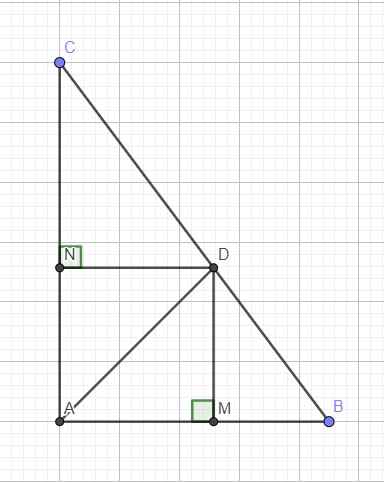
1: Xét tứ giác AMDN có
góc AMD=góc AND=góc MAN=90 độ
AD là phan giác
=>AMDN là hình vuông
2: BC=căn 3^2+4^2=5cm
AD là phân giác
=>DB/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=5/7
=>BD=15/7cm; CD=20/7cm