Tính giá trị nhỏ nhất của P= x2 + 3x+12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Phương pháp:
- Tìm TXĐ
- Tính y’
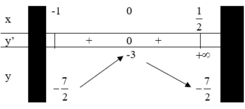
- Lập bảng biến thiên của hàm số trên đoạn - 1 ; 1 2
- Xác định giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Tính tích M.m.
Cách giải:
TXĐ: D = R\{1}
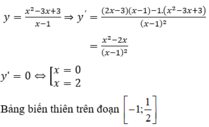
![]()
![]()

Đáp án C
Ta có y ' = 2 x x - 1 - x 2 - 3 x - 1 2 = 0 ⇔ [ x = - 1 x = 3
Lập BBT ⇒ M = f - 1 = - 2 m = f 0 = - 3 ⇒ P = - 5
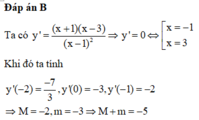

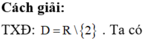
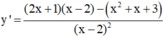
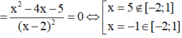
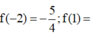
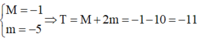
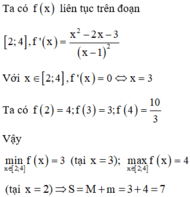
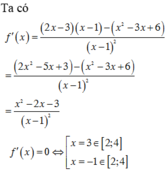
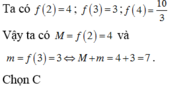
\(P=x^2+3x+12\)
\(=\left(x^2+2\cdot\frac{3}{2}\cdot x+\frac{9}{4}\right)-\frac{9}{4}+12\)
\(=\left(x+\frac{3}{2}\right)^2+\frac{39}{4}\ge\frac{39}{4}\)Vì \(\left(x+\frac{3}{2}\right)^2\ge0\forall x\)
Dấu "=" xảy ra <=> \(\left(x+\frac{3}{2}\right)^2=0\Leftrightarrow x=-\frac{3}{2}\)
Vậy \(P_{min}=\frac{39}{4}\) tại \(x=-\frac{3}{2}\)
GTNN là \(\frac{-3}{2}\)