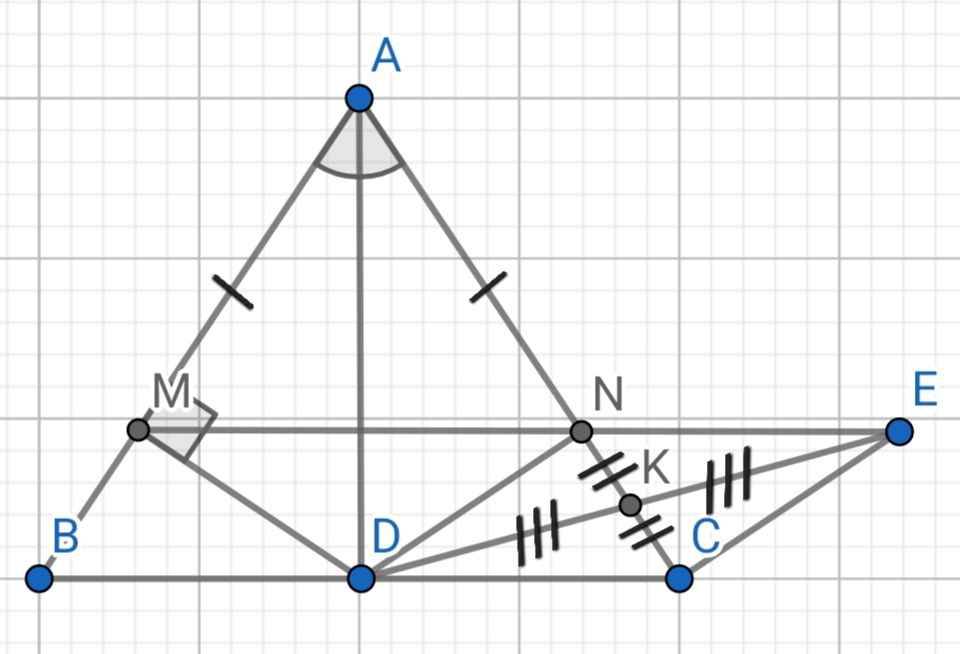
Cho tam giác ABC cân tại A có AD là đường phân giác a, CM tam giác ADB = tam giác ADC b, kẻ DM vuông góc với AB tại M, DN vuông góc với AC tại N. CM tam giác DMN cân c, Lấy điểm P sao cho D là trung điểm của đoạn thẳng NP. CM đường thẳng BC là đường trung trực của đoạn thẳng MP d, Gọi MP cắt BC tại K, NK cắt MD tại I. CM AD,MN,IP cùng đi qua một điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó:ΔABD=ΔACD
b: Xét ΔADM vuông tại M và ΔADN vuông tại N có
AD chung
\(\widehat{DAM}=\widehat{DAN}\)
DO đó: ΔADM=ΔADN
Suy ra: DM=DN
hay ΔDMN cân tại D
c: Ta có: AM=AN
DM=DN
Do đó: AD là đường trung trực của MN
hay AD⊥MN

 a) Do AD là tia phân giác của ∠BAC (gt)
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Do ∆ABC cân tại A
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
⇒ BD = CD
⇒ D là trung điểm của BC (1)
Do ∆ABD = ∆ACD (cmt)
⇒ ∠ADB = ∠ADC (hai góc tương ứng)
Mà ∠ADB + ∠ADC = 180⁰ (kề bù)
⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰
⇒ AD ⊥ BC (2)
Từ (1) và (2) ⇒ AD là đường trung trực của BC
b) Sửa đề: Chứng minh ∆ADM = ∆ADN
Do ∠BAD = ∠CAD (cmt)
⇒ ∠MAD = ∠NAD
Xét ∆ADM và ∆ADN có:
AD là cạnh chung
∠MAD = ∠NAD (cmt)
AM = AN (gt)
⇒ ∆ADM = ∆ADN (c-g-c)
⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)
⇒ DN ⊥ AN
⇒ DN ⊥ AC
d) Do K là trung điểm của CN (gt)
⇒ CK = KN
Xét ∆DKC và ∆EKN có:
CK = KN (cmt)
∠DKC = ∠EKN (đối đỉnh)
KD = KE (gt)
⇒ ∆DKC = ∆EKN (c-g-c)
⇒ ∠KDC = ∠KEN (hai góc tương ứng)
Mà ∠KDC và ∠KEN là hai góc so le trong
⇒ EN // CD
⇒ EN // BC (3)
∆AMN có:
AM = AN (gt)
⇒ ∆AMN cân tại A
⇒ ∠AMN = (180⁰ - ∠MAN) : 2
= (180⁰ - ∠BAC) : 2 (4)
∆ABC cân tại A (gt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC (6)
Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng

Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già Tôi bị bê đê con dê già

a: góc ABC=90-30=60 độ
góc DBM=180-45-60=75 độ
góc DCN=45+30=75 độ
b: Xét ΔDNC vuông tại N và ΔDBM vuông tại M có
DC=DB
góc DCN=góc DBM
=>ΔDNC=ΔDBM
=>DM=DN
c: Xét tứ giác AMDN có
góc AMD=góc AND=góc MAN=90 độ
DM=DN
=>AMDN là hình vuông
=>AD là phân giác của góc BAC
a: Xét ΔADB và ΔADC có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔABD=ΔACD
b: Xét ΔAMD vuông tại M và ΔAND vuông tại N có
AD chung
góc MAD=góc NAD
=>ΔMAD=ΔNAD
=>MD=DN
=>ΔDMN cân tại D