Hai ca nô làm việc đưa thư giữa hai bến sông A và B dọc heo bờ sông như sau: hàng ngày vào lúc quy định hai ca nô rời bến A và B chạy đến gặp nhau, trao đổi bưu kiện cho nhau rồi quay trở lại. Nếu hai ca nô cùng rời bến một lúc thì ca nô từ A phải mất 1,5 giờ mới trở về bến A, còn ca nô từ B phải đi mất 2,5 giờ mới trở về bến B. Biết rằng hai ca nô có cùng tốc độ đối với nước v1 không đổi và nước chạy với vận tốc v2 không đổi. Bỏ qua thời gian trao đổi bưu kiện a) So sánh vận tốc trung bình của mỗi ca nô trên cả quãng đường đi và về b) Muốn cho hai ca nô đi mất thời gian như nhau thì ca nô B phải xuất phát muộn hơn ca nô ở A một khoảng thời gian bằng bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian khi ca nô B xuất phát từ bến là t (giờ), khi đó thời gian ca nô A đã đi được là t+1,5.
Khi gặp nhau, khoảng cách hai ca nô đã đi được bằng nhau, ta có:
v × (t+1,5) = v × 3 - v × t
=> v × (t+1,5+t) = 3v
=> v × (2t+1,5) = 3v
=> t = (3-1,5) : 2 = 0,75
Vậy, để hai ca nô đi mất thời gian bằng nhau, ca nô ở B phải xuất phát muộn hơn ca nô ở A 0,75 giờ (tức 45 phút).

đề bị sai rồi xuất phát cùng lúc mà cùng vận tốc , => gặp nhau giữa AB
=> s= nhau
ta có s , t cùng lúc,v (= nhau )
mà thời gian đi khác nhau là sao ?
Bởi vì nước chảy nên cano này xuôi dòng thì cano kia ngược dòng và ngược lại
do vậy nên vận tốc bị thay đổi dẫn đến chênh lệch thời gian

Cái câu "trở về đến bến" dễ gây hiểu lầm ghê, đọc sơ thì 1,5h như là thời gian đi từ A đến B và đi từ B về A vậy, nhưng trong trường hợp này phân tích kỹ thì nó chỉ là thời gian đi từ A đến B thôi
Quãng đường AB dài:
\(\left\{{}\begin{matrix}S=\left(v_1+v_2\right).1,5\\S=\left(v_1-v_2\right).2,5\end{matrix}\right.\) \(\Rightarrow v_{tb}=\frac{S}{t}=\frac{S}{1,5+2,5}\)
b/ Câu b có vấn đề rồi bạn, thời gian của chúng sẽ vẫn là như vậy cho dù chúng có xuất phát muộn hơn hay sớm hơn. Như thế này mới hợp lí:" Tìm vận tốc của cano 1 và cano 2 đối với nước để chúng đi mất thời gian là như nhau"
bạn giải thích rõ hơn đc ko tạ sao vtb lại như thế

Gọi vận tốc ca nô là x(km/h), x > 3. Vận tốc ca nô xuôi dòng là x + 3(km/h)
Thời gian ca nô xuôi dòng từ A đến B là 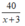 (giờ)
(giờ)
Vận tốc ca nô ngược dòng là x - 3 (km/h)
Quãng đường ca nô ngược dòng từ B đến địa điểm gặp bè là : 40 - 8 = 32 km
Thời gian ca nô ngược dòng từ B đến địa điểm gặp bè là: 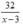 (giờ)
(giờ)
Thời gian bè trôi là:
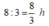
Ta có phương trình:
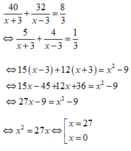
So sánh với điều kiện thì chỉ có nghiệm x = 27 thỏa mãn, suy ra vận tốc của ca nô là 27km/h.
Chọn đáp án C

Gọi x là vận tốc của ca nô ( km/h; x>0)
Vận tốc ca nô đi xuôi : x+3
Vận tốc ca nô đi ngược: x-3
Thời gian ca nô đi xuôi từ A đến B là: \(\dfrac{40}{x+3}\left(h\right)\)
Thời gian ca nô đi ngược từ B đến khi gặp bè là: \(\dfrac{32}{x-3}\left(h\right)\)
Thời gian bè trôi đến khi gặp ca nô là \(\dfrac{8}{3}\)
Ta có pt: \(\dfrac{40}{x+3}+\dfrac{32}{x-3}=\dfrac{8}{3}\)
\(\Leftrightarrow120\left(x-3\right)+96\left(x+3\right)-8\left(x+3\right)\left(x-3\right)\Leftrightarrow8x^2-216x=0\Leftrightarrow x=27\)(tmđk) Vậy vận tốc của ca nô là 27km/h


Cho nơi gặp nhau của hai xe là C, Đặt AC=s1 CB=s2 AB=s1+s2
Vận tốc trung bình của ca nô A là:
\(\upsilon_{tbA}=\dfrac{2s_1}{t_A}=\dfrac{2s_1}{t_1+t_1}=\dfrac{2s_1}{\dfrac{s_1}{\upsilon_1+\upsilon_2}+\dfrac{s_2}{\upsilon_1-\upsilon_2}}=\dfrac{\upsilon^2_1-\upsilon^2_2}{\upsilon_1}\) (1)
Vận tốc trung bình của ca nô B là:
\(\upsilon_{tbB}=\dfrac{2s_2}{t_B}=\dfrac{2s_2}{t_2+t_2}=\dfrac{2s_2}{\dfrac{s_2}{\upsilon_1-\upsilon_2}+\dfrac{s_2}{\upsilon_1+\upsilon_2}}=\dfrac{\upsilon^2_1-\upsilon^2_2}{\upsilon_1}\) (2)
Từ (1) và (2) \(\Rightarrow\upsilon_{tbA}=\upsilon_{tbB}\)