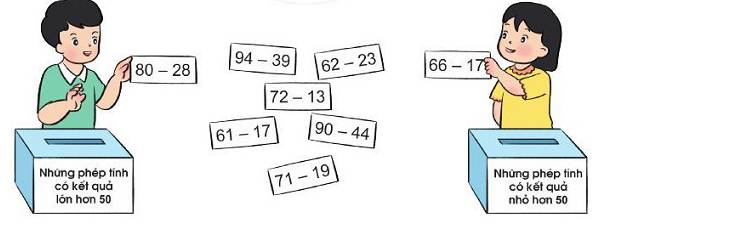
Chọn thẻ ghi phép tính thích hợp cho mỗi hộp:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 11 2023
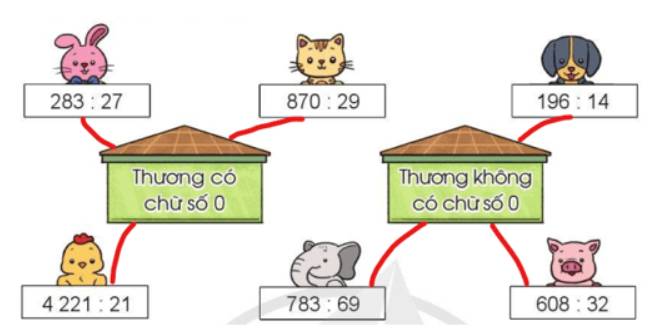
Ta có:
283 : 27 = 10 (dư 13)
870 : 29 = 30
196 : 14 = 14
4 221 : 21 = 201
783 : 69 = 11 (dư 24)
608 : 32 = 19
27 tháng 11 2023
a: \(\dfrac{5}{9}\cdot\dfrac{4}{6}=\dfrac{5\cdot4}{9\cdot6}=\dfrac{20}{54}=\dfrac{10}{27}\)
\(\dfrac{1}{3}\cdot\dfrac{5}{12}=\dfrac{1\cdot5}{3\cdot12}=\dfrac{5}{36}\)
b:
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
24 tháng 7 2023
Mèo: 2 kg
Voi: 5 tấn
Chó: 1 yến
Hươu cao cổ: 9 tạ
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
a. Không gian mẫu: \(C_{10}^3\)
Số cách chọn 3 số nguyên liên tiếp: 8 cách (123; 234;...;8910)
Số cách chọn ra 3 số trong đó có đúng 2 số nguyên liên tiếp:
- Cặp liên tiếp là 12 hoặc 910 (2 cách): số còn lại có 7 cách chọn
- Cặp liên tiếp là 1 trong 7 cặp còn lại: số còn lại có 6 cách chọn
Vậy có: \(C_{10}^3-\left(8+2.7+7.6\right)=56\) bộ thỏa mãn
Xác suất: \(P=\dfrac{56}{C_{10}^3}=...\)
b.
Có 2 số chia hết cho 4 là 4 và 8
Rút ra k thẻ: \(C_{10}^k\) cách
Số cách để trong k thẻ có ít nhất 1 thẻ chia hết cho 4: \(C_{10}^k-C_8^k\)
Xác suất thỏa mãn: \(P=\dfrac{C_{10}^k-C_8^k}{C_{10}^k}>\dfrac{13}{15}\)
\(\Leftrightarrow\dfrac{2}{15}>\dfrac{C_8^k}{C_{10}^k}=\dfrac{\dfrac{8!}{k!\left(8-k\right)!}}{\dfrac{10!}{k!\left(10-k\right)!}}=\dfrac{\left(9-k\right)\left(10-k\right)}{90}\)
\(\Leftrightarrow\left(9-k\right)\left(10-k\right)-12< 0\Leftrightarrow k^2-19k+78< 0\)
\(\Rightarrow6< k< 13\)
Ta có:
80 – 28 = 52 ; 52 > 50.
94 – 39 = 55 ; 55 > 50.
62 – 23 = 39 ; 39 < 50.
66 – 17 = 49 ; 49 < 50.
61 – 17 = 44 ; 44 < 50.
72 – 13 = 59 ; 59 > 50.
90 – 44 = 46 ; 46 < 50.
71 – 19 = 52 ; 52 > 50.
Vậy:
• Những phép tính có kết quả lớn hơn 50 là 80 – 28; 94 – 39; 72 – 13; 71 – 19.
• Những phép tính có kết quả nhỏ hơn 50 là 62 – 23; 66 – 17; 61 – 17; 90 – 44.