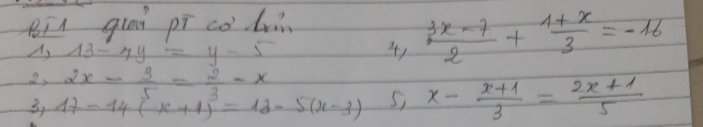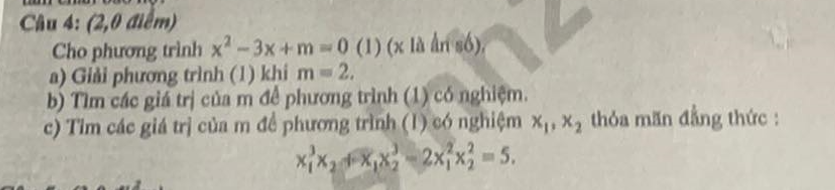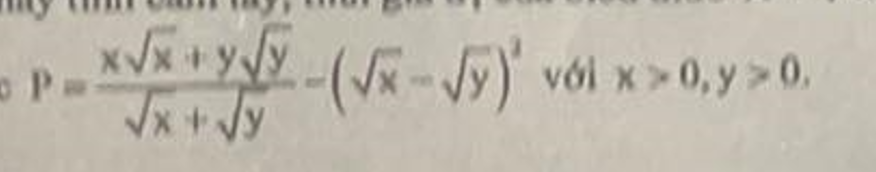Plss giups với cần gấp:(
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(VT=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{2\left(\sqrt{3}-1\right)}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(\dfrac{\sqrt{7}+\sqrt{5}}{2}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)=\dfrac{7-5}{2}=\dfrac{2}{2}=1\)
=VP
b: \(VT=3-\sqrt{5}+2\left(\sqrt{5}+1\right)-\left|\sqrt{5}-2\right|\)
=3-căn 5+2căn 5+2-căn 5+2
=3+2+2=7
=VP

1" =>-4y-y=-5-13
=>-5y=-18
=>y=18/5
2: =>2x+x=2/3+3/5
=>3x=19/15
=>x=19/45
3: =>17-14x-14=13-5x+15
=>-14x+3=-5x+28
=>-9x=25
=>x=-25/9
4: =>3(3x-7)+2(x+1)=-96
=>9x-21+2x+2=-96
=>11x=-96+19=-77
=>x=-7
5: =>15x-5x-5=6x+3
=>10x-5=6x+3
=>4x=8
=>x=2




a) thay m=2 vào pt (1) ta có
\(x^2-3x+2=0\)
<=>\(\left(x-1\right)\left(x+2\right)=0\)
<=>\(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
b)để pt (1) có 1 nghiệm
<=>\(\Delta=0\)
<=>9-4m=0
<=>m=\(\dfrac{9}{4}\)
KL: vậy để pt (1) có 1 nghiệm thì m=\(\dfrac{9}{4}\)
c)để pt có 2 nghiệm pb thì \(\Delta>0\)
<=>9-4m>0
<=>m<\(\dfrac{9}{4}\)
áp dụng định lý Vi-ét ta có \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m\end{matrix}\right.\)
theo đề bài ta có \(x_1^3x_2+x_1x_2^3-2x_1^2x_2^2=5\)
<=>\(x_1x_2\left(x_1+x_2\right)^2-4x^2_1x^2_{2^{ }}=5\)
<=>\(9m-4m^2=5\)
<=>\(4m^2-9m+5=0\)
<=>\(\left(m-1\right)\left(4m-5\right)=0\)
<=>\(\left[{}\begin{matrix}m=1\\m=\dfrac{5}{4}\end{matrix}\right.\)
KL: vậy với m =1 hoặc m=\(\dfrac{5}{4}\) thì pt có 2 nghiệm pb thỏa yêu cầu đề bài

\(P=\dfrac{\left(\sqrt{x}\right)^3+\left(\sqrt{y}\right)^3}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}-\sqrt{y}\right)^2\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}{\sqrt{x}+\sqrt{y}}-\left(x-2\sqrt{xy}+y\right)\)
\(=x-\sqrt{xy}+y-x+2\sqrt{xy}-y\)
\(=\sqrt{xy}\)

2A
4D
5C
6D
7D
8:
Bởi vì nhân vật “tôi” đã nhận ra sự thay đổi của bức tường và nghĩ rằng thời gian sẽ làm phai nhòa đi hết tất cả những kỉ niệm và căn phòng chính là nơi lưu giữ kỉ niệm của người đến trước và người đến sau.

a) Ta có: BC//AD(gt)
Mà \(AD\perp AB\)(gt)
=> BC⊥AB
\(\Rightarrow\widehat{ABC}=90^0\)
b) Ta có: BC//AD(gt)
\(\Rightarrow\widehat{C_2}=\widehat{D_1}=110^0\)(đồng vị)
\(\Rightarrow\widehat{C_1}=180^0-\widehat{C_2}=180^0-110^0=70^0\)(l=kề bù)
c) Ta có: \(\widehat{BCD}=\widehat{C_2}=110^0\)(đối đỉnh)
\(\Rightarrow\widehat{BCI}=\dfrac{1}{2}\widehat{BCD}=55^0\)(do CI là phân giác góc BCD)
Ta có:BC//AD(gt)
\(\Rightarrow\widehat{BCI}+\widehat{AIC}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{AIC}=180^0-\widehat{BCI}=180^0-55^0=125^0\)