Cho O là trung điểm của đoạn thẳng AB có độ dài bằng 2a. Trên cùng 1 nửa mặt phẳng bờ là đường thẳng AB vẽ 2 tia Ax, Ay cùng vuông góc với AB. Trên tia Ax lấy điểm D bất kỳ, qua điểm O vẽ đường thẳng vuông góc với DO tại O cắt By tại C.
1) Chứng minh tam giác ADO đồng dạng với tam giác BOC.
2) Chứng minh DO là tia phân giác của góc ADC.
3) Vẽ OH vuông góc với CD ( H thuộc CD ). Gọi I là giao điểm của AC và BD, E là giao điểm của AH và CO. Chứng minh 3 điểm E, I, F thẳng hàng.

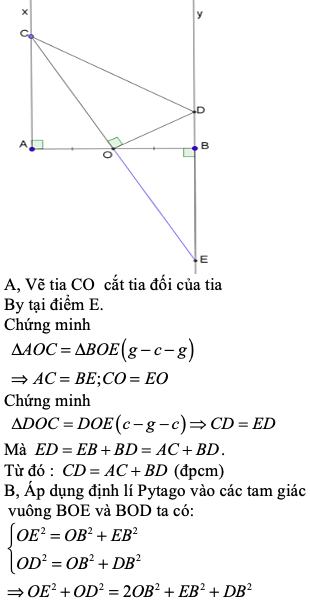
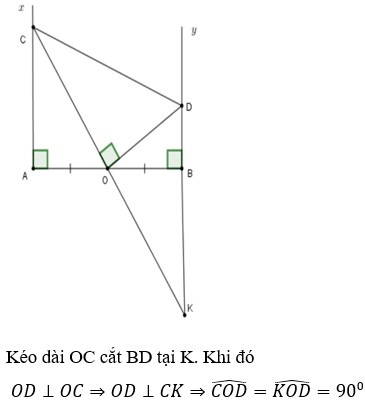





1:Gọi giao của DO và CB là H
Xét ΔOAD vuông tại A và ΔOBH vuông tại B có
OA=OB
góc AOD=góc BOH
=>ΔOAD=ΔOBH
=>OD=OH
=>ΔCDH cân tại C
=>ΔAOD đồng dạng với ΔBOH
Xét ΔBOH vuông tại B và ΔOCH vuông tại O có
góc BHO chung
=>ΔBOH đồng dang với ΔOCH
=>ΔAOD đồng dạng với ΔOCH
2: ΔCHD cân tại C
=>góc CDH=góc CHD=góc ADH
=>DH là phân giác của góc ADC
Cảm ơn bạn nha