Phân tích thành nhân tử: x3+y3+z3-3xyz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 12 2017
x 3 + y 3 + z 3 – 3xyz = x + y 3 – 3xy(x + y) + z 3 – 3xyz
= [ x + y 3 + z 3 ] - [ 3xy.(x+ y) + 3xyz]
= [ x + y 3 + z 3 ] – 3xy(x + y + z)
= (x + y + z)[ x + y 2 – (x + y)z + z 2 ] – 3xy(x + y + z)
= (x + y + z)( x 2 + 2xy + y 2 – xz – yz + z 2 – 3xy)
= (x + y + z)( x 2 + y 2 + z 2 – xy – xz - yz)
CM
8 tháng 8 2019
a) 16(12 t 2 +1).
b) Gợi ý x 3 + y 3 = ( x + y ) 3 - 3xy(x + y)
(x + y - z)( x 2 + y 2 + z 2 - xy + xz + yz).
16 tháng 5 2023
a: =(x+y)^3+z^3-3xy(x+y)-3xyz
=(x+y+z)(x^2+2xy+y^2-xz-yz+z^2)-3xy(x+y+z)
=(x+y+z)(x^2+y^2+z^2-xy-xz-yz)
b: a+b+c<>0
A=(a+b+c)^3-a^3-b^3-c^3/a+b+c
=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)/(a+b+c)
=a^2+b^2+c^2-ab-ac-bc
=1/2[a^2-2ab+b^2+b^2-2bc+c^2+a^2-2ac+c^2]
=1/2[(a-b)^2+(b-c)^2+(a-c)^2]>=0
NH
1
19 tháng 9 2021
\(a,=\left(2x-5\right)\left(x+1\right)\\ b,=\left(x-10\right)\left(x+1\right)\\ c,=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
CM
11 tháng 12 2019
a) 12x. b) 4xy
c) 2y(3 x 2 + y 2 ).
d) (x + y + z)( x 2 + y 2 + z 2 – xy – xz - yz).
T
1 tháng 9 2023
\(\left(x+y-z\right)^3-x^3-y^3+z^3\)
\(=\left[\left(x+y\right)-z\right]^3-x^3-y^3+z^3\)
\(=\left(x+y\right)^3-z^3-3\left(x+y\right)z\left(x+y-z\right)-x^3-y^3+z^3\)
\(=x^3+y^3-z^3+3xy\left(x+y\right)-3\left(x+y\right)z\left(x+y-z\right)-x^3-y^3+z^3\)
\(=3xy\left(x+y\right)-3z\left(x+y\right)\left(x+y-z\right)\)
\(=3\left(x+y\right)\left[xy-z\left(x+y-z\right)\right]\)
\(=3\left(x+y\right)\left(xy-zx-yz+z^2\right)\)
\(=3\left(x+y\right)\left[x\left(y-z\right)-z\left(y-z\right)\right]\)
\(=3\left(x+y\right)\left(y-z\right)\left(x-z\right)\)
#\(Urushi\text{☕}\)
MD
1 tháng 9 2023
Áp dụng (a+b)3 = a3+b3+3ab(a+b), ta có:
(x+y+z)3-x3-y3-z3
=[(x+y)+z]3-x3-y3-z3
=(x+y)3+z3+3z(x+y)(x+y+z)-x3-y3-z3
=x3+y3+3xy(x+y)+z3+3z(x+y)(x+y+z)-x3-y3-z3
=3(x+y)(xy+xz+yz+z2)
=3(x+y)[x(y+z)+z(y+z)]
=3(x+y)(y+z)(x+z)
BH
1
13 tháng 8 2020
Ta có: ( x - y) z3 + ( y - z ) x3 + ( z - x ) y3
= ( x - y ) z3 + ( y - z )x3 + ( z - y)y3 + ( y - x ) y3
= ( x - y ) ( z3 - y3 ) + ( y - z ) ( x3 - y3)
= ( x - y ) ( z - y ) ( z2 + zy + y2 ) + ( y - z ) ( x - y) ( x2 + xy + y2 )
= ( x - y ) ( y - z ) ( x2 + xy + y2 - z2 - zy - y2)
= ( x - y ) ( y - z ) [ ( x2 - z2) + ( xy - zy) ]
= ( x - y ) ( y - z ) [ ( x - z ) ( x + z ) + y ( x - z ) ]
= ( x - y ) ( y - z ) ( x - z ) ( x + y + z )
BH
1
13 tháng 8 2020
(x - y).z3 + (y - z).x3 + (z - x).y3
= z3(x - y) + x3y - x3z + y3z - xy3
= z3(x - y) + xy(x2 - y2) - z(x3 - y3)
= z3(x - y) + xy(x - y)(x + y) - z(x - y)(x2 + xy + y2)
= (x - y)(z3 + x2y + xy2 - x2z - xyz - y2z)
= (x - y)[z(z2 - x2) + xy(x - z) + y2(x - z)]
= (x - y)[z(z - x)(z + x) - xy(z- x) - y2(z - x)]
= (x - y)(z - x)(z2 + xz - xy - y2)
= (x - y)(z - x)[(y - z)(y + z) - x(y - z)]
= (x - y)(z - x)(y - z)(y + z - x)
12 tháng 1 2023
a: (x+y+z)^3-x^3-y^3-z^3
=(x+y+z-x)(x^2+2xy+y^2-x^2-xy-xz+z^2)-(y+z)(y^2-yz+z^2)
=(x+y)(y+z)(x+z)
b: x^3+y^3+z^3=1
x+y+z=1
=>x+y=1-z
x^3+y^3+z^3=1
=>(x+y)^3+z^3-3xy(x+y)=1
=>(1-z)^3+z^3-3xy(1-z)=1
=>1-3z-3z^2-z^3+z^3-3xy(1-z)=1
=>1-3z+3z^2-3xy(1-z)=1
=>-3z+3z^2-3xy(1-z)=0
=>-3z(1-z)-3xy(1-z)=0
=>(z-1)(z+xy)=0
=>z=1 và xy=0
=>z=1 và x=0; y=0
A=1+0+0=1
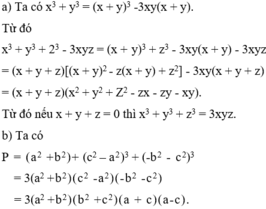
= (x + y)3 + z3 – 3x2y – 3xy2 - 3xyz
= (x + y +z)[(x + y)2 – (x + y)z + z2)] - 3xy(x + y + z)
= (x + y + z)(x2 +2xy + y2 – xz – yz +z2 – 3xy)
= (x + y + z)(x2 + y2 +z2 – xy - yz – xz)
x3 - y3 - z3 +3xyz
= (x3 - 3x2y +3xy2 -y^3) +3x2y-3xy2 - z3 +3xyz
= [(x-y)3 -z3] + 3x2y -3xy2 +3xyz
= (x-y-z)(x2 + 2xy+y2 +zx+zy + z2) + 3xy( x-y+z)
x3−y3−z3+3xyz=(x+y+z)(xy+yz+xz−x2−y2−z2) =-(x^3+y^3+y^3-3xyz)$
Ta tính x3+y2+z3−3xyz trước
ta có:
x3+y3+z3−3xyz=(x+y)3+z3−3xy(x+y)−3xyz=(x+y+z)(x2+y2+z2−xy−yz−xz)
=>x3−y3−z3+3xyz=(x+y+z)(xy+zy+xz−x2−y2−z2)