cho △ABC = △DEF. Biết A = 55°, số đo góc D bằng
A. 35°
B. 45°
C. 55°
D. 65°
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


cho tam giác MNP vuông tại M; biết N=35 độ ; số đo góc P là:
A 45 độ
B 55 độ
C. 65 độ
D 90 độ
\(\)+Tam giác MNP vuông tại M
\(=>\widehat{M}=90^o\)
+Áp dụng định lý tổng ba góc trong tam giác có:
\(\widehat{M}+\widehat{N}+\widehat{P}=180^o\)
\(=>\widehat{N}+\widehat{P}=180^o-\widehat{M}\)
\(=>\widehat{P}=180^o-\widehat{M}-\widehat{N}\)
\(=>\widehat{P}=180^o-90^o-35^o=55^o\)
=>Chọn B

\(\text{Câu 1: }=\widehat{B}+\widehat{C}=80^0\left(D\right)\\ \text{Câu 2:}\Delta ABC=\Delta DEF\left(A\right)\)

a) Có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)( tổng số đo 3 góc trong 1 tam giác)
\(55^o+35^o+\widehat{C}=180^o\)
\(\widehat{C}=180^o-90^o\)
\(\widehat{C}=90^o\)
b) Xét \(\Delta ABC\) vuông tại C có :
\(CB^2+AC^2=AB^2\) (định lý pi-ta-go)
\(49+AC^2=100\)
\(CA^2=51\)
\(CA=\sqrt{51}\approx7.14\)
a, Ta có : ^A + ^B = 900
Vậy ^C = 900
b, Vì ^C = 900
Vậy tam giác ABC vuông tại C
\(AC=\sqrt{AB^2-BC^2}=\sqrt{51}cm\)

\(a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)=5^3-3\cdot4\cdot5=65\left(A\right)\)

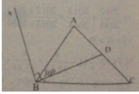
Tia BD nằm giữa hai tia BA và BC nên
A B C ^ = A D B ^ + D B C ^ ; D B C ^ = A B C ^ - A D B ^
D B C ^ = 55 ° - 30 ° = 25 °
Xét hai trường hợp
Trường hợp 1: Tia Bx và BD nằm trên
hai nửa mặt phẳng đối nhau có bờ là AB.
Ta có A B x ^ = D B x ^ - D B A ^ = 90 ° - 30 ° = 60 °
Trường hợp 2: Tia Bx và BD nằm cùng nửa mặt phẳng đối nhau có bờ là AB.
Ta có A B x ^ = D B x ^ + D B A ^ = 90 ° + 30 ° = 120 °

A B C D E F 5 7 8 12 45 55
Giải
Vì\(\Delta ABC~\Delta DEF\) nên ta có:
\(\widehat{D}=\widehat{A}=45^o\)
\(\widehat{E}=\widehat{B}=55^o\)
\(\widehat{F}=\widehat{C}=\left(180^o-45^o-55^o\right)=80^o\)
Xét\(\Delta ABC~\Delta DEF\) có:
\(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{2}{3}\)
\(\Rightarrow DE=\frac{AB.3}{2}=7,5\)
\(DF=\frac{AC.3}{2}=10,5\)
#hoktot<3#
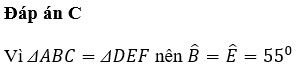
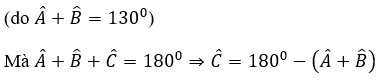
Vì Tam giác `ABC =` Tam giác `DEF`
`->`\(\widehat{A}=\widehat{D}=55^0\)
`-> C`
ΔABC=ΔDEF
\(=>\widehat{A}=\widehat{D}\) mà \(\widehat{A}=55^o\)
\(=>\widehat{D}=55^o\)
=>Chọn C